En la última clase mencioné el experimento de Taylor-Couette, que tiene una serie de inestabilidades muy estudiadas, con una ruta que lleva eventualmente a la turbulencia completamente desarrollada. El experimento es relativamente sencillo: dos cilindros concéntricos, con un fluido en medio. El cilindro interno se gira con velocidad angular Ω, y al aumentar de a poco la velocidad angular (y en número de Reynolds, Re) primero se obtiene un flujo laminar, luego aparece una inestabilidad que genera un nuevo flujo con rollos con simetría de rotación, luego esa simetría se rompe y se genera otra solución en la que los rollos forman un ángulo con el plano horizontal, luego hacen un zig-zag, luego aparece otra inestabilidad, y así hasta terminar con un flujo muy desordenado.
En este video se ve el experimento, aunque Ω aumenta muy rápido por lo que es difícil reconocer cada bifurcación:
Por otro lado, este video es muy lento, pero se ve claramente cada solución (pueden ir adelantando; presten atención a los rollos en 0:28 y 0:40, el zig-zag en 1:40, y la evolución posterior):
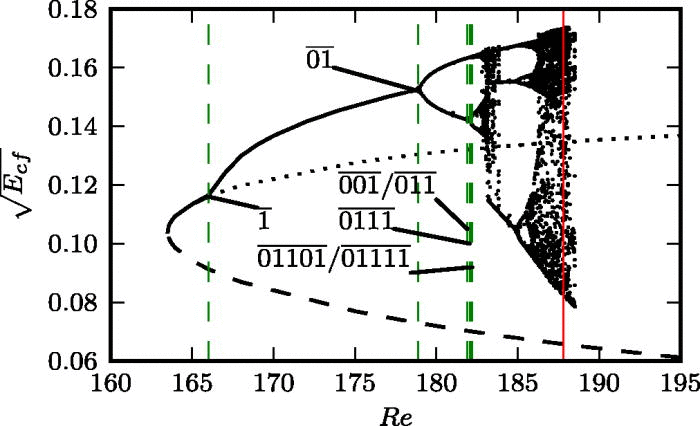
El diagrama de bifurcaciones de este sistema (hoy en clase veremos algo parecido para el problema que estudió Lorenz) es el siguiente:
La figura, tomada de T. Kreilos y B. Eckhardt, “Periodic orbits near onset of chaos in plane Couette flow”, Chaos 22, 047505 (2012), muestra la amplitud del flujo transversal al flujo laminar (que apunta en la dirección de rotación del cilindro interno) en función del número de Reynolds. Cada bifurcación marca la aparición de una nueva solución.