A partir de hoy tendremos clases en los horarios y aulas usuales de la materia. Es decir, la práctica de 14 a 17 hs en el laboratorio 1103 del edificio Cero-Infinito, y la teórica de 17 a 19 hs en el aula 1206 del mismo edificio.

En la última clase vimos que los invariantes ideales (es decir, las magnitudes conservadas en el límite ideal y sin fuerzas externas) de las ecuaciones que describen un fluido incompresible dependen de la dimensionalidad del problema. En tres dimensiones tenemos una sola magnitud conservada (la energía cinética), mientras que en dos dimensiones tenemos dos magnitudes conservadas (la energía cinética y la enstrofía). Como adelanté en clase, vamos a ver que el número de magnitudes invariantes tiene un fuerte efecto en los patrones y las soluciones que aparecen en estos sistemas. A modo de ilustración, a continuación pueden ver una imagen de una simulación numérica de un flujo turbulento en tres dimensiones:

Lo que ven en amarillo son regiones con mucha vorticidad. Los paneles (de izquierda a derecha y de arriba hacia abajo) muestran zoom sucesivos del flujo en las regiones indicadas en blanco en el panel previo. Noten como el flujo tiende a generar estructuras de vorticidad muy pequeñas, generando desorden.

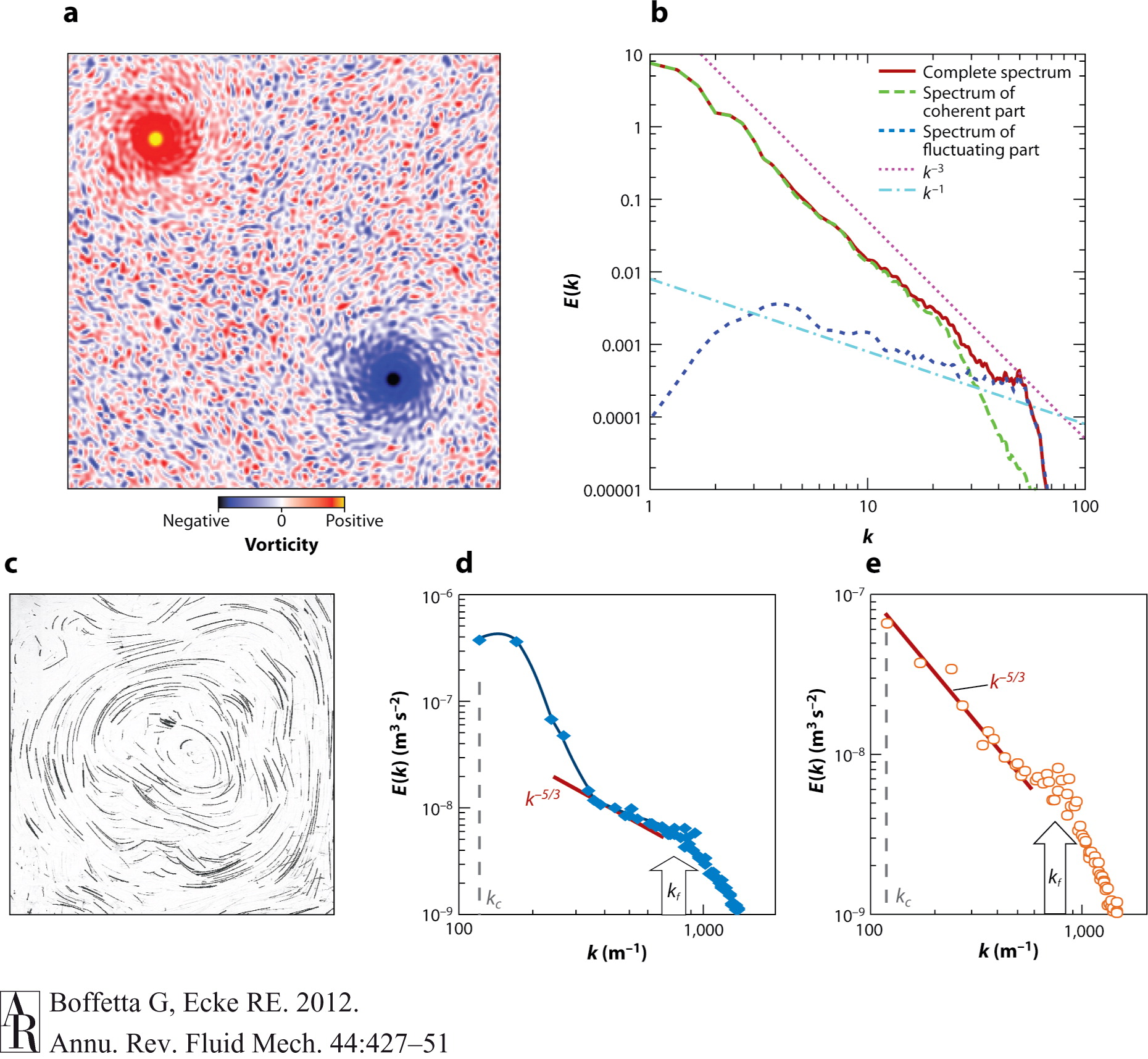
En dos dimensiones la situación es muy diferente:

No se preocupen por ahora por los espectros que se ven a la derecha de esta figura. Pero noten, a la izquierda, la distribución de espacial de vorticidad (a). A diferencia del caso tridimensional, se forman espontáneamente estructuras ordenadas con dos grandes vórtices. Aunque las ecuaciones físicas son las mismas, el cambio en el número de magnitudes conservadas explica la diferencia entre los patrones emergentes. Y aunque esto no es suficiente para entender los patrones macroscópicos que observamos en atmósferas planetarias, el efecto de la dimensionalidad del flujo no es despreciable: