Este video es una simulación que hizo Nahuel de una memoria de un bit que falla por fluctuaciones térmicas. Para los que quieran saber más o repasar lo que aprendimos ayer, ahí van las slides de la charla. Por otro lado, lo que Nahuel comentó al final de la charla, la segunda ley emergente que permite caracterizar estados estacionarios de no equilibrio, fue publicado en Nature Communications y es un paper de acceso abierto, lo pueden encontrar acá.

Cuando un sistema está en equilibrio, sabemos cuál es la probabilidad de cada microestado: e^{-βH}/Z. Ésa es la distribución de Boltzmann. Pero qué pasa cuando el sistema está en un estado estacionario que no es de equilibrio, como la barra de la imagen? Cuál es la probabilidad de cada microestado en esa situación? Ésa es una pregunta abierta de la termodinámica de no equilibrio, y de los avances recientes para responder a esa pregunta nos va a hablar uno de sus protagonistas: Nahuel Freitas, este miércoles en el horario de la práctica, en la primera charla de expertos del curso. No se la pierdan que es un lujo!

Acá tienen un review muy claro sobre relaciones de trabajo, escrito por el propio Jarzynski. Y éste es el Nature de 2005 donde se comprobó experimentalmente el teorema de Crooks en el plegado de macromoléculas. Otro review sobre relaciones de trabajo, más enfocado en su aplicación a motores moleculares, es éste. En ese review, el foco no está puesto en las identidades de Jarzynski y Crooks sino en otra, la de Gallavotti y Cohen. Buscando referencias donde se hablara de la aplicación del teorema de Crooks a motores moleculares, encontré este artículo, muy claro y ameno, cuyo autor les va a resultar familiar.

En la clase de ayer hablamos del demonio de Maxwell, y vimos que un ingrediente fundamental para reconciliar a ese ser con la segunda ley de la termodinámica es el principio de Landauer: el borrado de un bit de memoria a temperatura T conlleva la emisión de un calor mayor o igual a kT log 2 (acá tienen el artículo original de Landauer). La conexión entre el principio de Landauer y el demonio de Maxwell es obra de Charles Bennett, que escribió este artículo de divulgación sobre el tema en Scientific American que recomiendo leer, es muy claro y ameno. En clase también discutimos que el principio de Landauer por sí solo no es suficiente para reconciliar al demonio con la segunda ley. Hay que asumir además que el demonio (la memoria en el ejemplo de la máquina de Szilard) no absorbe calor en el proceso de medida, es decir, en el paso de 2 a 3 de la figura.

Y en ese proceso la entropía de la memoria aumenta (pasa de 0 a k log 2), así que, en principio, la segunda ley le da margen para absorber calor. En clase comenté por arriba un argumento para descartar esa posibilidad, y quiero aprovechar este espacio para dar algo más de detalle sobre ese argumento. La clave es que, en el proceso de medida, la memoria (m) se correlaciona con la máquina (M), y en consecuencia la entropía del sistema memoria + máquina, que en general es S(mM) = S(m)+S(M|m), no es simplemente suma de entropías como suele pasar en termodinámica. La segunda ley para el sistema mM nos dice que el calor absorbido Q cumple

Q/T ≤ ΔS(mM) = ΔS(m) + ΔS(M|m).

En el proceso de medida tenemos ΔS(m) = k log 2. Cuánto vale ΔS(M|m)? Inicialmente, conocer el estado de la memoria no nos dice nada sobre el estado del gas; en particular, el gas podría estar en cualquier mitad de la caja. En cambio, después de la medida conocer el estado de la memoria sí nos dice algo sobre el estado del gas: nos dice en qué mitad está. Por lo tanto, ΔS(M|m) = -k log 2, así que el calor absorbido en el proceso de medida cumple

Q/T ≤ 0,

como queríamos ver. Esto está bien explicado en las secciones 9.1 y 9.2 del libro An introduction to stochastic thermodynamics, de Naoto Shiraishi (es uno de los libros de la bibliografía del curso).

Un último comentario. Fíjense que, en los argumentos que usamos para reconciliar al demonio con la segunda ley, usamos la segunda ley. Ésa es una crítica que a veces se le hace a este tipo de argumentos. Pero para mí eso no es un problema. Estamos haciendo un test de consistencia, viendo si la aplicación de la segunda ley en distintas fases de un experimento imaginario nos lleva a una contradicción con esa misma ley.

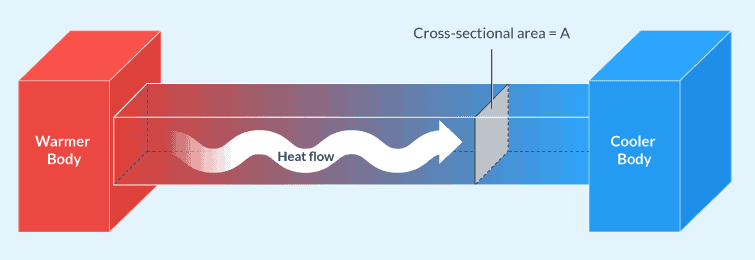
Como dijimos ayer, este año se cumplen 75 años del artículo “A mathematical theory of communication”, piedra fundacional de la teoría de la información y obra cumbre de Claude Shannon, que es el de la foto (por lo visto, era muy aficionado a hacer malabares y andar en monociclo). El artículo es muy ameno, se recomienda su lectura; lo pueden encontrar acá. Uno de los principales resultados del artículo es el teorema de “source-coding”, que es el que discutimos ayer en la práctica y hace unos días en la teórica: el mínimo número de bits por caracter necesarios para codificar los mensajes de una fuente es la entropía por caracter de esa fuente. El otro resultado principal es el teorema de “noisy channel coding”, que ayer en la práctica comentamos muy por arriba. De este teorema quiero hablar en este post.

La idea es la siguiente: un emisor envía mensajes a través de un canal ruidoso, de forma que los mensajes se pueden corromper por el camino. Cómo hacemos para asegurarnos de que el receptor recibe el mensaje correcto? La idea más sencilla es la de la repetición: si le quiero mandar un bit a alguien (0 o 1) y quiero asegurarme de que va a recibir la información correctamente, le mando por ejemplo tres copias del mensaje (000 o 111). Así, si una de las copias se corrompe por el camino, el receptor va a poder leer el mensaje igualmente. Por ejemplo, si recibe 010 va a interpretar que yo le había mandado 000 y el segundo bit se corrompió, y va a tener una buena probabilidad de acertar. Pero está claro que no va a poder estar 100% seguro de acertar. Quién te dice que no se corrompieron 2 bits en el camino, que en realidad el mensaje original era 111 y fueron el primero y el tercero los que se corrompieron? Bueno, para reducir la probabilidad de error podemos enviar cuatro copias del mensaje en lugar de tres, o más aún. Claro que cuando aumentamos la redundancia, si bien reducimos la probabilidad de error, la comunicación se vuelve más lenta, menos eficiente. Surge entonces la pregunta: si queremos que la probabilidad de error sea cero, tenemos que mandar un mensaje infinitamente redundante? Nótese que, a más redundancia, más previsible se vuelve el caracter promedio, o menos informativo, y por lo tanto disminuye la entropía por caracter. Entonces, podemos reformular la pregunta de la siguiente forma: si queremos que la probabilidad de error sea cero, tenemos que mandar un mensaje con entropía cero, es decir, que no sea nada informativo? La respuesta es no: hay un umbral, llamado la capacidad del canal de comunicación, tal que, si la entropía cae por debajo de ese umbral, existe una forma de codificar el mensaje con la que la probabilidad de errores es despreciable. Ése es el segundo teorema de Shannon.

La capacidad del canal es algo simple. El canal está caracterizado por una distribución de probabilidad condicionada: la probabilidad p(x|y) de que el mensaje enviado por el emisor sea x dado que el receptor leyó y (si no hubiera ruido, esta probabilidad sería 1 para x=y, y 0 para cualquier otro x). Con esta distribución, junto con la distribución de probabilidad que caracteriza al emisor (cuya entropía nos da el mínimo número de bits necesarios para codificar sus mensajes) nos podemos calcular la entropía condicional S(X|Y), la incertidumbre acerca del mensaje enviado (X) conocido el mensaje recibido (Y). La información mutua

I(X,Y)=S(X)-S(X|Y)

es una medida de cuánta información sobrevive al ruido: es la información contenida en el mensaje enviado (S(X)) menos la incertidumbre del receptor sobre cuál es ese mensaje (S(X|Y)). Bueno, la capacidad del canal es el máximo de la información mutua sobre todos los posibles emisores.

El teorema de Shannon nos dice que, siempre que la entropía del emisor caiga por debajo de la capacidad del canal, habrá alguna forma de codificar el mensaje que garantice que no va a haber errores. Ahora, cuál es ese código es otra historia, y por lo visto tuvieron que pasar muchos años hasta que se encontraron los primeros ejemplos.