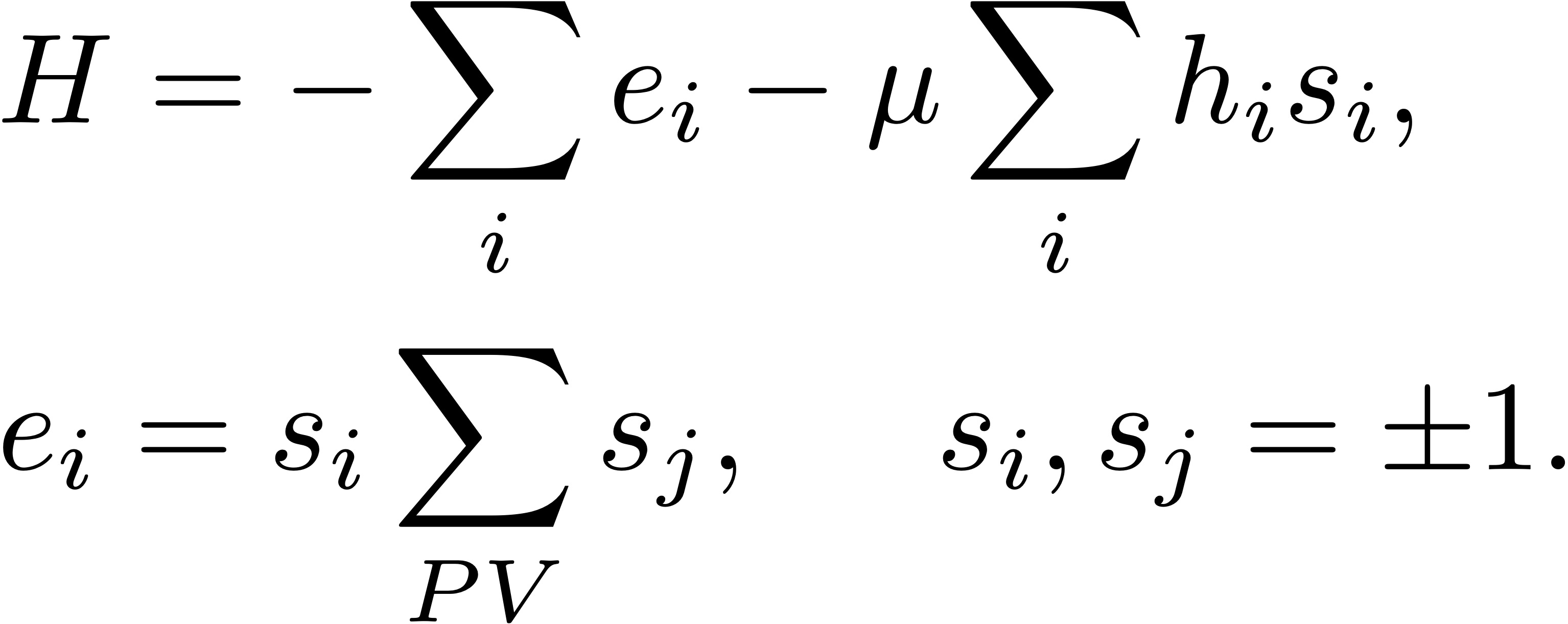Ex Machina (disponible en Netflix) es una película de 2014 con algunos giros de tuerca inquietantes alrededor de la idea de construir máquinas con inteligencia artificial. Y, sorprendentemente, los temas de esta materia tienen una relación cercana con este problema. El premio Nobel de Física 2021 fue otorgado a Giorgio Parisi, Syukuro Manabe y Klaus Hasselmann por contribuciones fundamentales a la comprensión de los sistemas complejos. Y en particular, la mitad del premio Nobel fue para Giorgio Parisi, entre otras cosas, por sus aportes al estudio de los vidrios de spin. Los vidrios de spin son un modelo sencillo para sistemas magnéticos amorfos, un caso en cierto sentido más general que el de los modelos de Ising que estamos considerando en el curso.
Ustedes podrán preguntarse qué relación hay entre vidrios de spin e inteligencia artificial. Comencemos por un problema más sencillo (o tal vez mucho más difícil): el juego de Go. El Go es un juego de mesa, pariente del ajedrez, en el que dos jugadores ponen piedras blancas o negras en turnos, en cualquier lugar del tablero, en una cuadrícula de 19×19 puntos. El objetivo del juego es rodear la mayor cantidad de territorio posible con las piedras del color del jugador.
Las reglas son muy sencillas: (1) Una piedra sin libertades (es decir, completamente rodeada por piedras del color opuesto) es capturada y removida del tablero. (2) No se pueden hacer jugadas que recreen la situación previa del tablero. Y (3) cuando un jugador pasa su turno dos veces seguidas, el juego termina. A pesar de esta simpleza (o tal vez como resultado de la misma), es un juego muy complejo. El número de posiciones legales en el tablero es mayor a 10170 , muchísimo más grande que en el ajedrez, y más grande que el número de átomos en el universo. Como resultado, los métodos para hacer que computadoras jueguen al Go calculando todas las jugadas posibles (como se hace con el juego de ajedrez) son inviables. Así, el juego de Go resulta un desafío más que interesante para la inteligencia artificial.
Hasta hace unos años, uno de los métodos preferidos para programar computadoras para jugar al Go era aplicar el método de Montecarlo para encontrar configuraciones del tablero que minimicen la energía (o el Hamiltoniano) de un modelo de Ising que tuviera alguna relación con las reglas del juego de Go y con las condiciones para ganar una partida. Por ejemplo, un posible Hamiltoniano es el siguiente, donde si es el color de las piedras en cada posición (+1 o -1 para blanco o negro), hi es el número de libertades de la piedra i-ésima (cuantos casilleros tiene libre alrededor), PV indica que la suma se hace sobre los primeros vecinos, y μ (>0) es una “energía” que premia las configuraciones en las que las piedras propias (+1) tienen libertades (es decir, no están rodeadas):
¡De pronto el modelo de Ising encuentra aplicaciones muy lejos de la física de materiales magnéticos! Sin embargo, estos métodos resultan en programas de Go que juegan apenas tan bien como un jugador humano mediocre. Y cuando el problema de jugar bien al Go parecía inaccesible para las computadoras, Google presentó en 2016 una red neuronal profunda que le ganó a todos los grandes campeones humanos del juego.
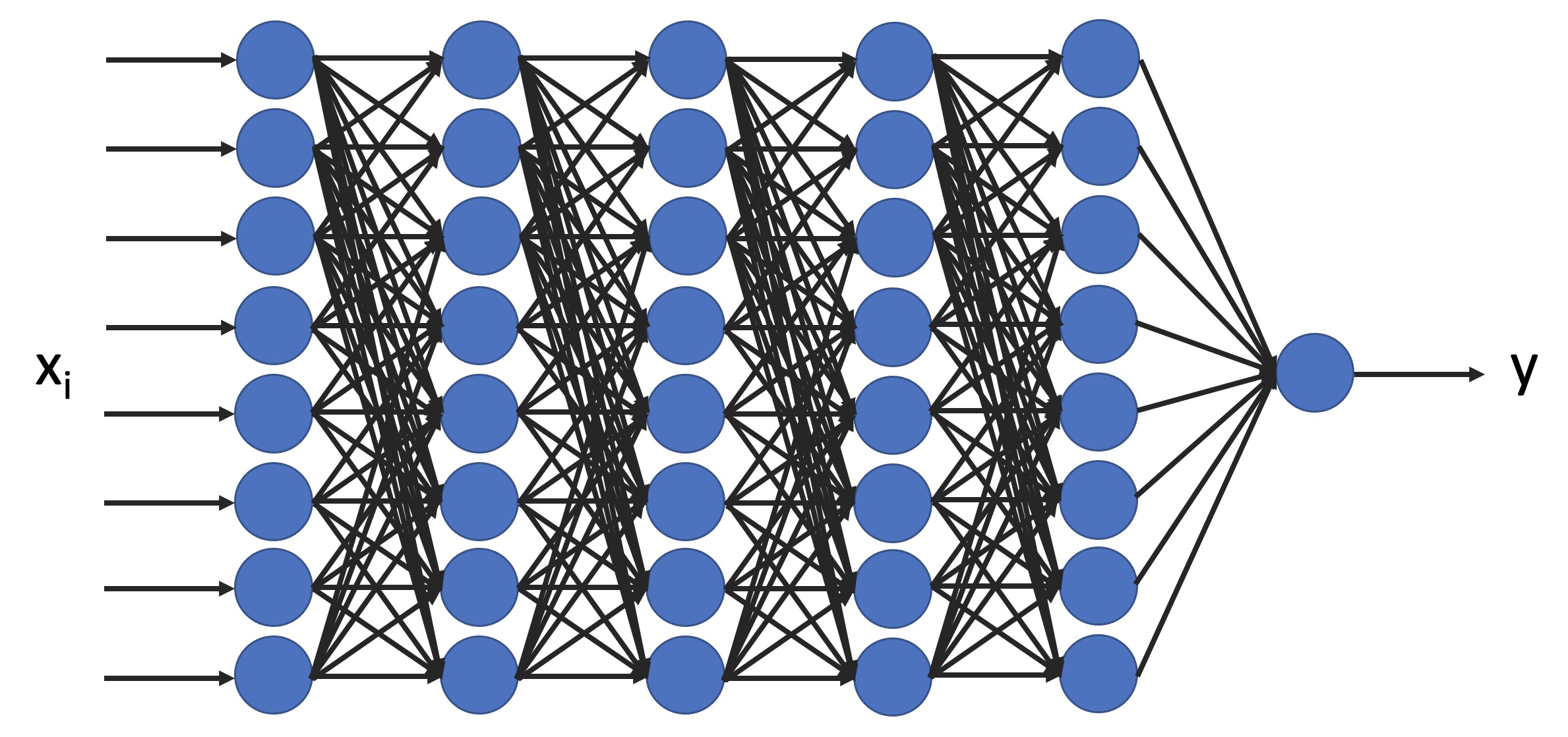
Una red neuronal profunda es una red con muchas capas de neuronas artificiales: los datos ingresan (en la siguiente figura, por la izquierda), son multiplicados por coeficientes (llamados “pesos”) en cada conexión entre neuronas, y el resultado es procesado con alguna operación sencilla por cada neurona (que puede estar “activada” o “inactivada”). El procedimiento se repite en cada capa de neuronas, hasta que se obtiene un resultado final (por dar un ejemplo muy crudo y simplificado, ingresa el estado actual del tablero de Go y obtenemos como resultado la próxima jugada que conviene realizar):
Las redes neuronales son entrenadas con muchísimas jugadas, de forma tal de ajustar los pesos en cada una de las conexiones de las neuronas y obtener un resultado óptimo. Pero noten que la estructura de la red no es muy diferente a la de los sistemas magnéticos que estuvimos estudiando en el curso: tenemos nodos que interactúan con sus vecinos con algún coeficiente de acoplamiento, y su equilibrio corresponde al mínimo de alguna función (el error en la respuesta que obtenemos). La diferencia es que ahora esos coeficientes (los pesos) no están fijos, y pueden cambiar durante el entrenamiento.
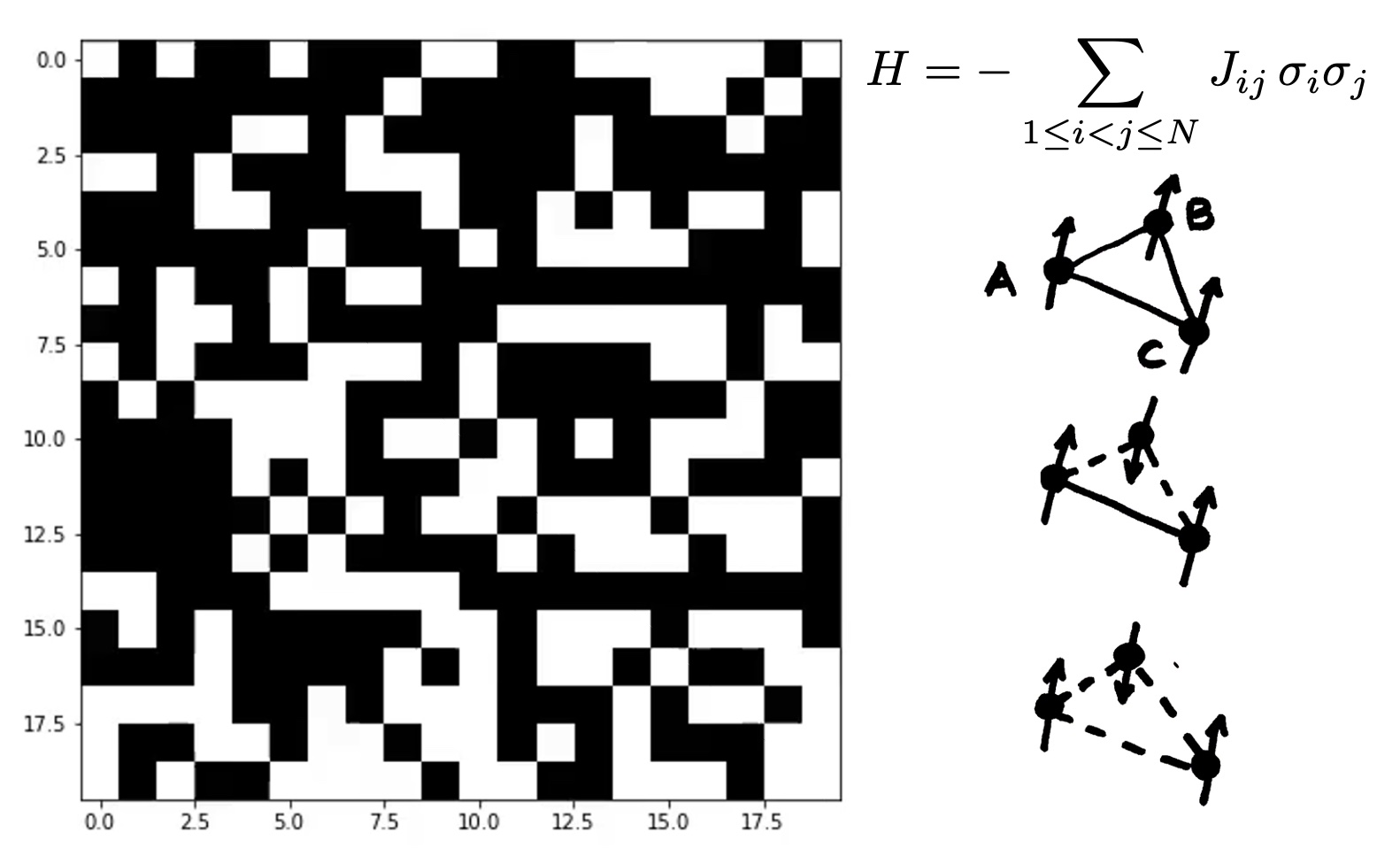
En física ocurre algo similar en materiales magnéticos amorfos. La estructura de la red de spines en esos materiales puede ser muy compleja, y los spines pueden interactuar con otros spines muy lejanos (en la peor situación posible, pueden interactuar todos contra todos). Y los spines pueden tener coeficientes de acoplamiento diferentes para cada par, que en la siguiente figura se indican como Jij para el acomplamiento del par (i,j). La variante de los modelos de Ising que se usa para estudiar este tipo de sistemas es conocida como vidrios de spin:
Los vidrios de spin son formalmente equivalentes a un tipo particular de redes neuronales (llamadas redes de Hopfield), pero muchos de los resultados que se obtuvieron para vidrios de spin se trasladan a la teoría de redes neuronales en forma muy general. Al construir la mecánica estadística de estos sistemas, la dificultad radica en que no solo es necesario armar ensambles con copias de todos los alineamientos posibles de los spines, sino que también es necesario armar réplicas del sistema con diferentes acoplamientos Jij (ya que uno no sabe cuánto valdrán los pesos, o los acoplamientos). Parisi hizo contribuciones muy relevantes que permitieron atacar este problema, y entender propiedades generales de los estados de equilibrio.
Los vidrios de spin, dada su complejidad, no tienen un único equilibrio: tienen una variedad muy grande de equilibrios posibles, que corresponden a mínimos locales de su energía libre. Así, la mecánica estadística de los vidrios de spin también nos da información sobre a qué estados posibles puede decaer una red neuronal durante el proceso de aprendizaje, o nos permite saber que ciertas redes neuronales pueden guardar “recuerdos”, y calcular la máxima cantidad de información que puede almacenarse en esas redes en función de su estructura, del número de neuronas, y del número de conexiones entre las neuronas.