Me parece interesante comentarles brevemente en este post cómo es posible obtener y visualizar flujos potenciales bidimensionales en el laboratorio.
Un montaje experimental comúnmente utilizado para producir y estudiar flujos potenciales bidimensionales es la celda de Hele-Shaw, introducida hace más de 100 años por Henry Hele-Shaw. Una celda de Hele-Shaw consiste esencialmente en el flujo de un líquido viscoso entre dos placas plano-paralelas ligeramente separadas entre sí.
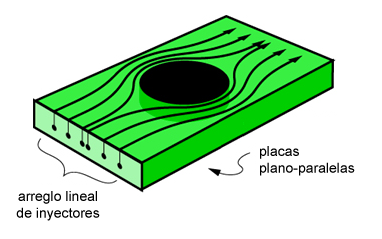La figura muestra un esquema simple de una celda de Hele-Shaw, ilustrando el flujo en torno de un obstáculo; un arreglo lineal para la inyección de colorante (como trazador) y algunas líneas de corriente a modo de visualización. El flujo dentro de la celda, laminar y paralelo, se conoce como flujo de Poiseuille plano y será objeto de estudio en la segunda mitad de la materia (en el marco de la guía de flujos viscosos).
Una propiedad paradójica de la celda de Hele-Shaw es que, a pesar de que el flujo es viscoso, las líneas de corriente bidimensionales que se observan tienen las propiedades de un flujo potencial. No se alarmen: más adelante en el curso veremos en detalle cómo probar esta afirmación.
Les dejo además un video que muestra el dispositivo experimental de Hele-Shaw y su operación. El obstáculo empleado (un cilindro en este caso) es ubicado en el pequeño espacio entre dos placas de vidrio dispuestas verticalmente. Un fluido viscoso y transparente se carga en un reservorio sobre la celda y se lo deja fluir a través de ella bajo la acción de la gravedad. El dispositivo cuenta además (como es usual) con un arreglo lineal de inyectores equiespaciados por donde se hace ingresar un fluido coloreado de iguales características (viscosidad, densidad, etc.). El reservorio se mantiene continuamente alimentado con fluido transparente y la visualización comienza haciendo ingresar el trazador al sistema. Para incrementar el contraste de las líneas observadas, se suele emplear un trazador fluorescente y trabajar a oscuras iluminando únicamente el flujo en la celda. Pueden visualizar el video haciendo click sobre la imagen asociada.
Finalmente, les dejo dos videos más: dos visualizaciones experimentales de las líneas de corriente de un flujo potencial bidimensional uniforme que enfrenta (a) un obstáculo cilíndrico y (b) un perfil alar; ambas obtenidas con la celda de Hele-Shaw mostrada en el primer video.
Hacer click sobre estas imágenes para ver los videos asociados.
