En la clase de hoy vimos que cuando se pretenden explorar las contribuciones de los términos con n > 1 en los desarrollos en serie de la exponencial que contiene la dirección de observación, los desarrollos multipolares para fuentes pequeñas y campo lejano se vuelven inmanejables. Si además estamos interesados en explorar la zona intermedia, no hay otro remedio que recurrir a las expresiones rigurosas obtenidas en los sistemas de coordenadas adecuados a cada simetría del problema. Estas soluciones se pueden expresar también como series de multipolos, los más conocidos y usados son los llamados armónicos esféricos vectoriales, el libro de Jackson los trata en el capítulo 16. Lean lo que dice Jackson en la introducción de dicho capítulo:

o sea, que estos desarrollos multipolares en armónicos esféricos vectoriales no solo sirven para describir la radiación producida por fuentes localizadas sino también para resolver problemas de radiación con contornos (algo parecido a lo que hicimos con los otros desarrollos multipolares cuando discutimos por qué el cielo es azul).
En este trabajo del Journal of Optics que ya está en línea, pero que corresponde al fascículo de julio de esta revista, pdf acá, hemos empleado desarrollos multipolares (cilíndricos, en vez de esféricos) para predecir teóricamente la respuesta de alambres recubiertos por grafeno. Resulta que con el alambre recubierto de grafeno se obtienen efectos muy atractivos desde el punto de vista de muchísimas aplicaciones. Estos efectos serían imposibles de lograr con el alambre desnudo. Noten que si bien en el título del trabajo aparece la palabra “subwavelength”, el análisis no fue hecho con la aproximación de onda larga que vimos en el curso, sino con un análisis riguroso ya que estamos interesados en los campos cercanos (y no solo en el campo lejano). En la figura 2 del trabajo se comparan las secciones eficaces para el alambre desnudo y para el alambre con grafeno y con distintos valores de los voltajes de compuerta (en la figura están los potenciales químicos)
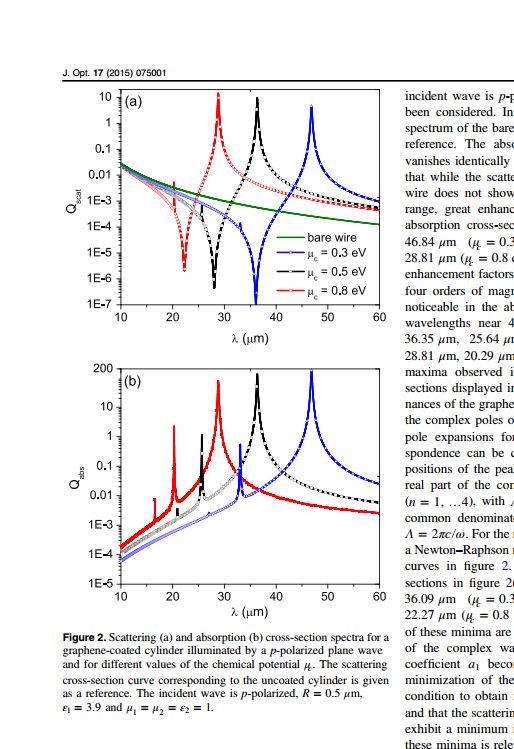
Como se cuenta en el trabajo, los picos corresponden a resonancias de plasmones superficiales localizados en la monocapa de grafeno. Y resulta que estas resonancias corresponden a frecuencias para las cuales se hacen casi singulares los términos de los desarrollos multipolares. Esto queda claro en la figura 3:
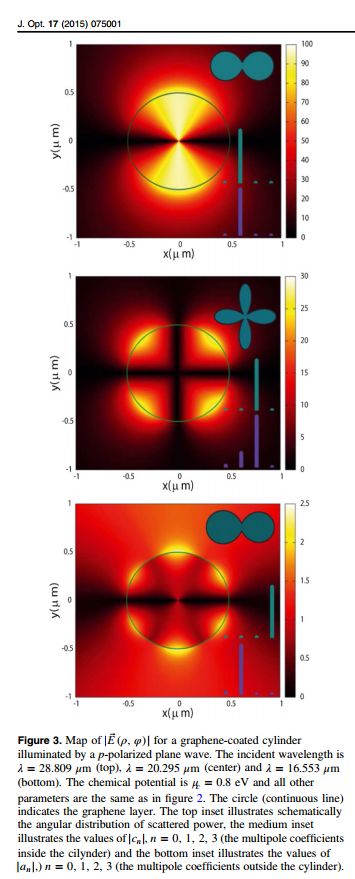
donde, entre otras cosas, se pueden observar distribuciones de cargas y corrientes dipolares (corresponden al término con n=1), cuadrupolares (corresponden al término con n=2) y hexapolares (corresponden al término con n=3). Un tema para pensar es la correlación (o no) entre estas distribuciones de cargas y corrientes y las distribuciones angulares de los campos lejanos, sugeridas por los esquemitas azules. Notar que la frecuencia de la onda incidente cambia dramáticamente las distribuciones de cargas y corrientes (y que el voltaje de compuerta permite elegir la posición de las resonancias, algo imposible sin grafeno).
Entre las líneas que estamos explorando en el área de estructuras con grafeno me gustaría mencionar i) la implementación de métodos más versátiles (y numéricamente más complicados que el que se cuenta en el paper) que nos permitan jugar con la geometría del alambre, ii) la propagación de plasmones en la dirección del eje del alambre (como si los alambres de grafeno fueran guías de onda), iii) la “hibridización” de resonancias plasmónicas (un concepto completamente análogo al de hibridización de orbitales moleculares) y iv) el estudio de sistemas multicapas periódicos, aperiódicos y aleatorios.