En un post de la última semana se habló de radiación cósmica de fondo, curvatura del espacio y agujeros negros. Quedó implícita la mención de que Maxwell también se impone en la relatividad general, obteniendo así las ecuaciones de Einstein-Maxwell. A fines de la década de 1960 se derivó, a partir de estas ecuaciones, que la solución de un agujero negro está completamente caracterizado por 3 observables: su masa, su momento angular y su carga eléctrica. Esto significa que toda otra información acerca de cómo se formó y lo que atravesó el horizonte de eventos queda clásicamente inaccesible para un observador externo. Se dice que un agujero negro no tiene pelos (aunque puede tener los 3 pelos de Homero en la imagen), porque no tiene ningún otro momento multipolar asociado. A este resultado se lo conoce como no-hair theorem, y junto con la radiación (cuántica) de Hawking, dan lugar a la paradoja de la pérdida de información.

En 1971, estando al tanto del teorema de agujeros negros sin pelos, Cohen y Wald plantearon el problema electrostático de una carga de prueba frente a un agujero negro de Schwarzschild de masa m (sin carga eléctrica, ni rotación). Ubicaron una carga q en el eje z para tener simetría azimutal y, tras unos pocos pasos intermedios, llegaron a la siguiente ecuación para el potencial electrostático en el espacio curvado por el agujero negro

Ecuación de Poisson en la geometría de Schwarzschild, donde J^0 representa la densidad de carga eléctrica de una carga puntual.

Notarán la similitud entre esta ecuación y la que plantearon en la clase teórica de la materia, usando coordenadas esféricas en el espacio plano. Cohen y Wald usaron separación de variables y expresaron el potencial con un desarrollo en Polinomios de Legendre, exactamente igual a lo que haríamos nosotrxs. La diferencia está en las soluciones radiales, hay un horizonte de eventos que complica un poco la solución, pero no mucho. Dejando de lado detalles, destacamos 2 cosas del  resultado de su artículo:

• El horizonte de eventos es una superficie equipotencial.
• Usaron la solución estática para estudiar qué pasa al acercar la carga lentamente hacia el agujero negro de Schwarzschild.

Sucesión de configuraciones estáticas (sin dinámica) de una carga de prueba q frente a un agujero negro de Schwarzschild. Al ubicar q sobre el horizonte sólo queda la carga total y desaparecen todos los otros momentos multipolares.

Las similitudes con un conductor esférico son asombrosas. Para completar la historia vale la pena mencionar que unos pocos años después se encontró que la expansión multipolar del potencial de una carga q frente a Schwarzschild se podía re-sumar en forma cerrada, el resultado fue presentado por B. Linet y es llamativamente simple:

Potencial para una carga "e" en Schwarzschild. Notar que al evaluar en m=0 se obtiene el potencial de una carga en el espacio Euclídeo vacío, idéntico a la ec.(88) del apunte FT1_práctica10

El primer término de arriba (azul en la figura) se obtuvo como una solución local de la carga en la geometría de Schwarzschild y se conoce como potencial de Copson, por el matemático que la publicó el en el año 1928. Copson olvidó imponer una condición de contorno asintótica, por lo que el resultado global era físicamente insatisfactorio y no se le dio mucha importancia. Casi 50 años después, Linet comprendió que la solución cerrada de Copson era correcta si sumaba el término φ_L (rojo en la figura), y mostró que el desarrollo de Cohen y Wald coincide con el potencial de Copson + Linet.

El  potencial φ_L que faltaba sumar en el año 1928 es un término monopolar necesario para quitar el exceso de carga a la solución de Copson y que el resultado refleje que Schwarzschild es un objeto sin carga eléctrica neta. Para eso lo que se usó fue el teorema de Gauss y así se garantizó que la carga total del problema fuera sólo q, la de la carga de prueba. La construcción que hizo Linet es completamente análoga a la que hacemos en los problemas externos a conductores esféricos cuando agregamos un término monopolar (“una carga en el centro”) para conseguir que quede un conductor descargado y que su superficie siga siendo equipotencial (recuerden los ítems (e) de los problemas 21 y 22,  FT1_práctica10).

Sucesión de configuraciones estáticas (sin dinámica): Equipotenciales de una carga de prueba frente a un agujero negro y frente a un conductor perfecto.

Mas allá de que faltaba un término monopolar, observen que φ_C  es -por sí solo- equipotencial sobre la superficie del horizonte de eventos (en unidades geométricas, esto es evaluar en r=2m, el horizonte). Además, en su artículo de 1928, Copson mencionó que “el potencial es independiente de la posición donde se ubique el electrón sobre la esfera del horizonte“, lo cual él calificó sencillamente como “a rather curious result“. Lo curioso del problema electrostático de la carga de prueba en la geometría de Schwarzschild es que predijo algo certero acerca de la calvicie eléctrica de los agujeros negros 40 años antes de que se formulara el teorema de agujeros negros sin pelos.

“No hay preguntas estúpidas“, es una de las enseñanzas que puede interpretarse de “El traje nuevo del emperador”, de Hans Christian Andersen.

La teoría y la práctica deben ir de la mano. En las clases de la práctica tenemos la tarea de ejercitar y aplicar los conceptos y herramientas que se aprenden en las clases teóricas. Ya vieron que son muchos ejercicios y muchas variantes, por eso, hay que dedicarle mucho tiempo. Además de los apuntes y los videos, continúen resolviendo los problemas individualmente. No es fácil ni poco, por eso, siempre aconsejamos que no pierdan el ritmo: traten de resolver todos los problemas de las guías y consulten a tiempo. Falta menos de un mes para la primera evaluación. (dato innecesario, quizás, para un sábado.)

Después del último posteo, y tratando de seguirle los pasos a la teoría, nos corresponde una mención inevitable: El vestido.

¿De qué color es el vestido? Algunx pensará que esta es una pregunta estúpida. Yo, mas bien, me siento un poco obvio tratando de introducir a el vestido. En resumen, la foto de arriba apareció hace 5 años en Tumblr. Luego circuló por todos lados porque gran parte del planeta se vio conmovidx por la ambigüedad en la percepción de los colores del vestido: algunxs ven azul y negro, otrxs ven blanco y dorado. Se trata de un ejemplo actual, viral, y paradigmático sobre la subjetividad y, también, sobre los factores cuantificables en relación a la interpretación que hacemos y a la percepción.

Las dos imágenes de Roger, en la primera foto del posteo, muestran cómo luce el vestido en una misma noche ante dos tipos distintos de iluminación. El vestido es el mismo, cambia la iluminación y/o la interpretación de nuestro cerebro. La foto del vestido, fue tomada por un teléfono celular, y quedó sobre expuesta: se iluminó el fondo de forma tal que el azul oscuro (original) del vestido quedó en un tono intermedio. Como consecuencia, “los valores objetivos” del color quedaron en gris azulado (en lugar de el azul) y marrón opaco (en lugar de el negro orignial). Esta es la clave de la ambigüedad. Antes de analizarla, veamos los cubos de abajo como otro ejemplo. El de la izquierda parece tener algunas tejas de color azul y otras de rojo, mientras que el de la derecha pareciera tener amarillos y rojos. Los azules y amarillos son, “en realidad”, grises.

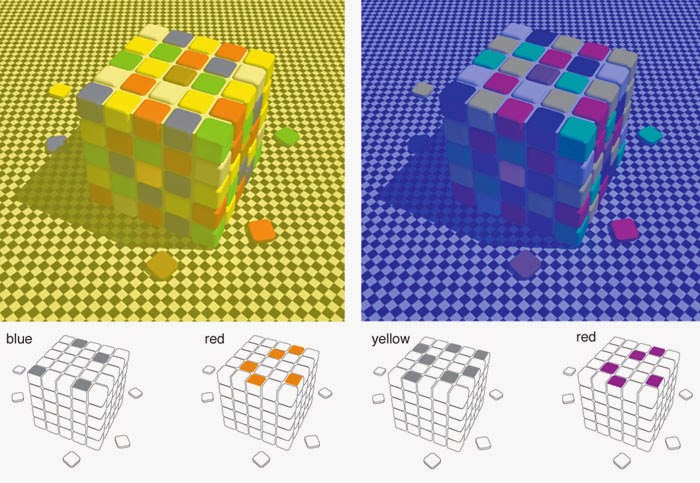
Dicho esto, pongamos en juego a dos factores fundamentales: el contraste y el contexto. En cuanto al contraste de color, nuestro cerebro suele interpretar como negro a la parte mas oscura de la imagen, por lo que seguramente encontremos negro en la foto del vestido cuando haya fondos claros en nuestro marco visual, y probablemente veamos otros colores cuando haya un negro oscuro en nuestro marco (las diferencias también cambian entre diferentes personas). El contexto, por su parte, tiene un rol asombroso para el cerebro, o mejor dicho, en nuestro cerebro: El vestido puede cambiar de color según cómo lo pensamos. Puede ser una tela blanca iluminada por un exterior azul, o una tela azul en una luz cálida. Además, el cerebro realiza constantemente un balance con la información que recibe para adaptar el color, es decir, resta la luz del ambiente para intentar ver un mismo objeto siembre “del mismo color”… pero, ya vimos, podemos engañarlo:

“No tiene por qué ser verdad lo que todo el mundo piensa que es verdad” (otra moraleja de “El traje nuevo del emperador”).

Por último, volviendo propiamente a FT1, cabe mencionar que en la guía 7 (de relatividad especial y formulación covariante del electromagnetismo) vamos a ver el cambio en la frecuencia (y longitud de onda) de la luz, debido al movimiento relativo entre la fuente y el observador. Este efecto, que es descripto por la teoría especial de la relatividad, se conoce como efecto Doppler relativista, es absolutamente cuantificable y no da lugar a la subjetividad -al menos- dentro del modelo y el paradigma correspondiente.

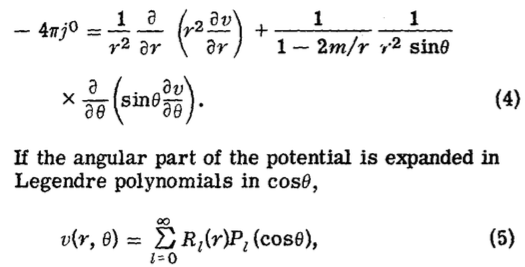
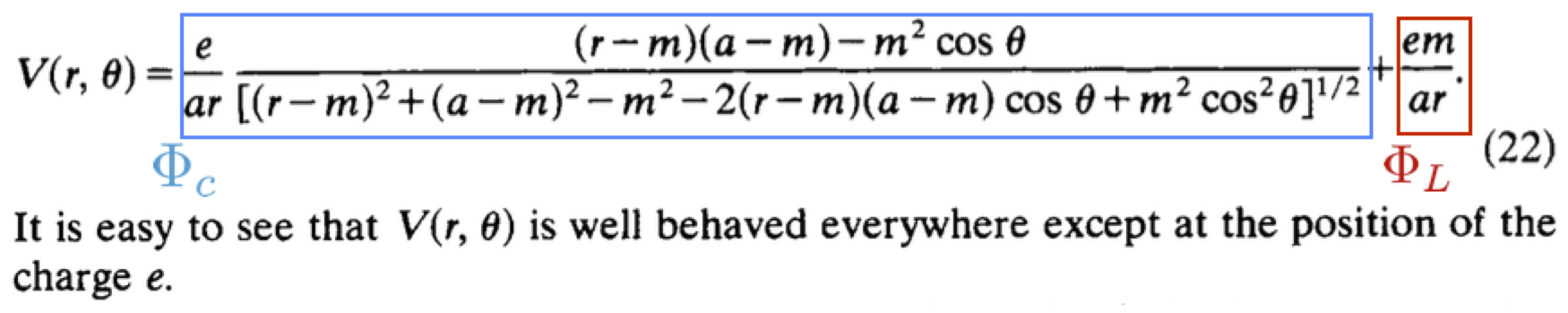
Ayer empezamos la guía 2 de separación de variables. Las guías irán apareciendo en su pestaña la semana previa a que comencemos a trabajarlas. En el cronograma pueden seguir, y anticiparse, a los temas de cada clase práctica y la modalidad (zoom, video, apunte, etc.). Además, cuando haya apuntes preparados para una clase por zoom, los vamos a subir temprano, o un día antes, en la pestaña de la práctica. Esto último es para que puedan descargarlo con comodidad y, si quieren, leerlos. De todas maneras, las explicaciones en zoom seguirán siendo pausadas y detalladas. Respecto a la clase de ayer (09/09), ya están subidos los videos: parte 1 y parte 2. Recuerden hacer todas sus consultas en los foros de la materia en el campus de exactas.