Hola a todos, el gran Nico Kovensky ha escrito estas notas donde explica con todo detalle cómo se resuelve el problema 10 de la guía de fermiones. Gracias Nico!
Author Archives: Guillermo Perez Nadal
El primer parcial y su resolución
Un gas de acero
Les comparto este interesante video que me ha hecho llegar el alumno Matías Senger,
https://www.youtube.com/watch?v=4Xx9omV7k3U
donde se ilustra de manera muy clara, mediante un “gas de bolitas de acero”, que la presión de un gas proviene de las colisiones de sus partículas con el recipiente.
Sobre el primer parcial
Les recordamos que el primer parcial será el miércoles 10 de mayo a las 17hs en el aula habitual de la práctica (aula 8). Se puede traer hoja de fórmulas (una carilla). Mucha suerte a todos!
Consultas primer parcial
Como ya anunciamos el miércoles en clase, hoy viernes 5 de mayo vamos a responder consultas en el bar, a partir de las 15hs (Nico va a estar a partir de las 14). Después, el lunes 8 de mayo vamos a dedicar las 5 horas de clase a consultas. Y además de eso, como saben, para cualquier otra consulta nos pueden escribir un mail o venir a ver a nuestras oficinas. Suerte!
Actualización de la guía 4
Como ya avisamos ayer en clase, hemos actualizado la guía 4: la nueva versión tiene dos problemas más (el 10 y 11), gentileza de Pablo Capuzzi, y además el problema 2 tiene varios items más.
Añadiendo complicación al problema 5 de combinatoria
Ayer una alumna nos hizo una pregunta interesante sobre el problema 5 de combinatoria, y se la transmito a todos: qué pasa si cada caja puede contener un máximo de k<N libros en lugar de N? Después de pensarlo un poco se nos ocurrió una respuesta para el caso libros indistinguibles, cajas distinguibles, asumiendo que k+1>N/2. A ver qué se les ocurre a ustedes!
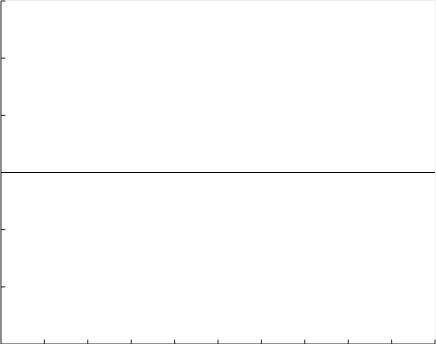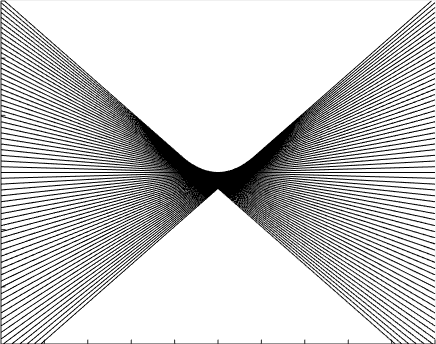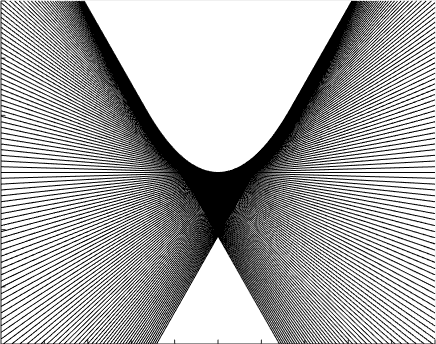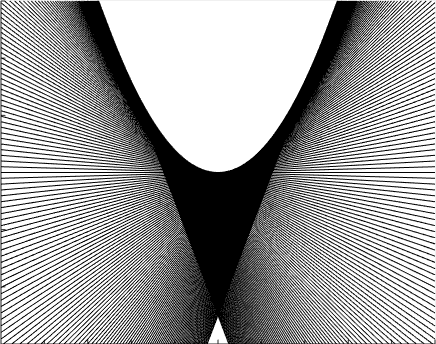
Invertibilidad de la transformada de Legendre
Ahí tienen un gif que hizo el alumno Marcos Wappner con muchas rectas (yo en el pizarrón había dibujado cinco) cuya pendiente y ordenada al origen están relacionadas como dicta la transformada de Legendre de la función f(x)=x^2. Como se ve claramente, estas rectas dibujan la parábola. Esto es un ejemplo gráfico del hecho general de que, si sabemos la transformada de Legendre de una función, entonces sabemos la función.