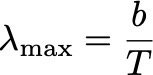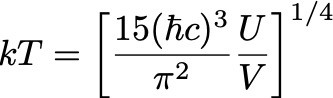La Guía 7, acerca del modelo de Ising, puede bajarse [aquí]. Por más que intentamos, no conseguimos ningún problema donde hubiera que calcular integrales.
Clase práctica del lunes 3/6
Caben muchos bosones en el estado fundamental. Ayer fue San Cono, lo que nos toca de cerca como físicos. Ayer también resolvimos en la práctica un problema fuera de guía, pero asiduo en los parciales: el problema del gas de bosones en una caja con gravedad. ¿Hay condensado? ¿No hay condensado? ¿Cuál es su aplicación en la reparación de relojes y, por qué no, en la relojería? Cuántas preguntas. [Aquí] pueden bajar el guion original de la clase de ayer. Trae extras. El ítem (d) es para medir fuerzas.
Quedó pendiente una versión 2024 1c de las notas de clase sobre condensados en una trampa armónica. Les dejo el apunte de la clase del cuatrimestre pasado, [aquí]. Pero también la serie de gráficos que mostramos durante la clase de la semana pasada, [aquí]. Son mucho mejores que los del apunte. Si estos gráficos no los convencen de que el nivel fundamental es el único que hay que separar al hacer la aproximación de sumas por integrales, entonces no sé cómo persuadirlos.
El problema del condensado en una trampa armónica nos sirvió de excusa para presentar la llamada aproximación semiclásica, que permite pasar de sumas sobre estados cuánticos a integrales en el espacio de fase clásico, sin necesidad de resolver la ecuación de Schrödinger. Llegamos a verlo en la clase de la trampa armónica, donde el espectro cuántico de energías es sencillo, y también lo vimos ayer en el problema del gas en la caja con gravedad, donde el espectro de energías es un horror. Me pareció oportuno escribir un apunte con las n maneras de aproximar por integrales la suma sobre estados para el caso de la trampa armónica, una de las cuales es la aproximación semiclásica. Pueden bajar el flamante apunte [aquí]. Incluye un apartado especial para los fundamentalistas de la densidad de estados. Algunas imágenes pueden producir convulsiones.
¡Eres un juguete!
El modelo de Ising es un modelo de juguete para el ferromagnetismo. Sin embargo, esto no significa que sea un modelo poco importante, o que solo tenga utilidad pedagógica. En cierto sentido, el modelo de Ising es el Buzz Lightyear de los modelos de juguete. El modelo, en su forma más sencilla y en dos dimensiones, consiste en un arreglo de espines (o dipolos magnéticos) que solo pueden tomar dos valores (+1 o -1). En ausencia de un campo magnético externo, los dipolos interactúan entre sí tratando de alinearse con sus vecinos más cercanos. A bajas temperaturas este arreglo de espines tiende a generar islas con la misma orientación, y si tenemos más espines con un signo que con el otro, entonces el material estará magnetizado. La transición entre el material no magnetizado y el material magnetizado, al bajar la temperatura, es una transición de fase similar (aunque no del mismo orden) a los cambios en los estados de agregación de la materia.
El desarrollo de la mecánica estadística entre fines del siglo XIX y principios del siglo XX, de la mano de Boltzmann y de Gibbs, permitió a los físicos comprender mejor varios sistemas y procesos (como el gas ideal, o los fenómenos de transporte), formalizar conceptos (como la noción de equilibrio, los microestados, el desorden, y la entropía), y estudiar fenómenos nuevos (como el condensado de Bose-Eistein, o la superfluidez y la superconductividad). Además, la mecánica estadística amplió el campo de aplicación de la física a otras áreas y a temas interdisciplinarios.
Sin embargo, aún en 1944 (más de 70 años después de la publicación de la ecuación de Boltzmann) no estaba claro si la mecánica estadística podría capturar y ayudar a comprender las transiciones de fase, como ocurren en la transición de agua líquida a vapor de agua, o en la magnetización espontánea de ciertos materiales (reales, no de juguete) al bajar su temperatura. Y aquí es donde el modelo de Ising, y Lars Onsager, abrieron las puertas a muchos desarrollos cruciales para la física en la segunda mitad del siglo XX. En 1944 Onsager encontró una solución exacta al modelo de Ising en dos dimensiones, calculando la función de partición del sistema, mostrando que podía sufrir una transición de fase y magnetizarse espontáneamente, y calculando la temperatura a la que ocurre la transición. La solución mostró por primera vez que las transiciones de fase aparecen como singularidades de las funciones termodinámicas del sistema, y convenció a los físicos de que la mecánica estadística podía ser usada para estudiar estos fenómenos. Fue tan relevante que al terminar la segunda guerra mundial, cuando varios físicos volvieron a la investigación básica, Hendrik Casimir le comentó en una carta a Wolfgang Pauli que estaba preocupado y dudaba de si podría volver a trabajar en física teórica luego de haber perdido contacto con el tema por tanto tiempo. Pauli (que era famoso por evaluar las teorías de sus colegas muy duramente) lo tranquilizó respondiendo que durante la guerra solo hubo un resultado que debía mirar: “No ha ocurrido mucho que sea de interés, excepto por la solución exacta de Onsager al modelo de Ising en dos dimensiones“.
Onsager es un personaje interesante. Muchos de sus resultados no fueron publicados en papers. La solución exacta al modelo de Ising apreció como una discusión de otro paper, su formula para la temperatura de la transición quedó en un pizarrón luego de un seminario que dió László Tisza, y la predicción de la cuantización de vórtices en un superfluido (luego redescubierta por Feynman) apareció en un paper resumiendo un seminario de otro investigador, en la sección de preguntas y respuestas del público.
Los que quieran jugar un poco con el modelo de Ising en 2D (antes de la práctica numérica), pueden mirar la siguiente página donde pueden simular el sistema con el método de Montecarlo, y variar la temperatura y el campo magnético externo. Para un campo externo igual a cero, prueben ver que pasa con la amplitud de las fluctuaciones en la magnetización si se acercan a la temperatura crítica (Tc ≈ 2.27) desde arriba (es decir, desde temperaturas altas):
Para terminar, no se pierdan el video en el que Onsager le explica a Ising que solo es un juguete:
La clase práctica del lunes, hoy [actualizado]
[Aquí] pueden bajar una versión taquigrafiada de la clase práctica del lunes, en donde resolvimos el problema 1 de la Guía 6. El ítem respecto a la presión necesitaba revisarse; pueden bajar la versión actualizada de la guía [aquí]. Al final de las notas hay algunos problemas propuestos.
La parte central del problema 1 es razonar la transición de fase. Ahora bien, una vez que lo entendieron, no es necesario aplicar paso por paso los mismos razonamientos a todo problema de condensación de Bose-Einstein que se les presente. No necesitan inventar continuamente la rueda. Lo digo porque en los parciales suelen hacer eso. La rueda ya la damos por inventada, vayan directamente al asunto.
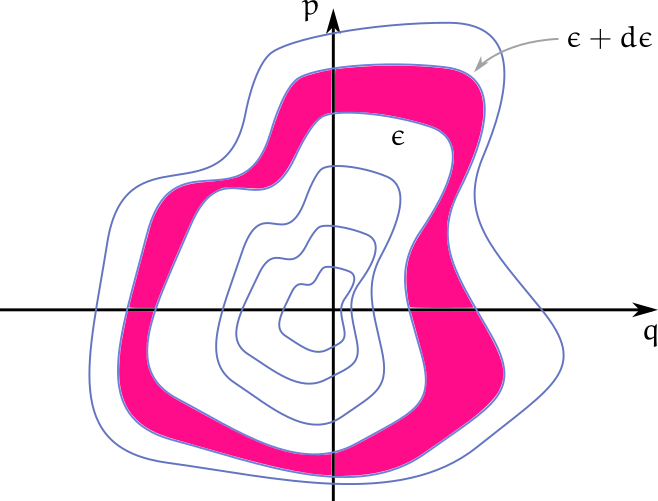
La condensación de Bose-Einstein tiene al menos dos puntos inciertos: el primero es la prescripción de separar en las sumas el término del nivel fundamental y aproximar el resto por una integral. El segundo es entender por qué hay una transición de fase y cómo toda la cuestión depende de manera decisiva de que se tome el límite termodinámico. Este segundo punto está explicado en el apunte de manera bastante formal, a diferencia de la mayoría de los argumentos que encontrarán en los libros. A primera vista, estos argumentos parecen suficientes, pero si se vieran en la necesidad de explicárselos a alguien, descubrirían, con gran azoramiento, que no son tan convincentes como creyeron. Como si repitieran en público un chiste y comprendiesen, cuando ya es demasiado tarde, que sólo lo recuerdan imperfectamente.
Respecto a la prescripción que indica separar la contribución del nivel fundamental y aproximar el resto por una integral, no tengo más que decir que es, como escribiría Lovecraft, intelectualmente repugnante.
En el único, único libro en donde he visto demostrado que esto tiene rigor matemático es en el de Pathria y Beale, en su apéndice F. Hasta cierto punto se entiende todo, pero después entra a jugar el resultado de un paper y la cosa se complica. Pero la demostración existe.
La prescripción de separar e integrar es difícil de justificar gráficamente para el caso del gas en una caja, porque se trata de una integral triple. Para el gas en una trampa armónica, uno puede transformar la suma triple en una suma simple. Como vimos el miércoles, entonces es evidente que la prescripción de separar e integrar es del todo razonable y justificada. El apunte sobre la clase del miércoles está en preparación. Mientras tanto, los urjo a leer las secciones sobre condensado en una trampa armónica en la edición de 2021 del libro de Pathria y Beale, aunque sólo el primero de ellos sea poeta urdu.
Síndrome del fluido normal
“¡Todos pueden ser súper! ¡Y cuando todos sean súper, nadie lo será!” La película Los increíbles (2004) tiene a uno de los villanos más interesantes de las películas de superhéroes. Syndrome no busca dominar al mundo, no desea poder o dinero. Desea que todos sean iguales, y que los superhéroes dejen de ser especiales. ¿Eso es algo bueno, no? ¿Por qué Syndrome sería entonces un villano? Sin embargo, al ver la película, algo parece incorrecto (y casi perverso) en pedirle a Dash con sus 10 años que no participe en el equipo de atletismo de su escuela porque sería excepcional. La película, que a primera vista parece un simple pasatiempo, plantea una discusión interesante sobre la excepcionalidad, la igualdad, y el festejo de la mediocridad.
Los superfluidos son excepcionales. Y algunas de las cosas que hacen son realmente increíbles. Un superfluido es un fluido que fluye sin viscosidad, lo que les permite atravesar canales muy delgados o medios porosos (por los que un fluido viscoso no podría pasar), o trepar por las paredes del recipiente que los contiene. El fenómeno de superfluidez se debe a la formación, a temperaturas muy bajas, de un condensado de Bose-Einstein en el que una fracción de los átomos que formal el fluido (usualmente Helio-4) dejan de tener agitación térmica (sin embargo, la teoría de condensados que vimos en clase corresponde a gases débilmente interactuantes, mientras que el Helio-4 superfluido es un líquido, con una energía potencial de interacción entre sus átomos que no es despreciable). El fenómeno está relacionado también con el de superconductividad.
El siguiente video, corto y muy recomendable, y que vimos rápidamente en clase, muestra varias de las propiedades más llamativas de los superfluidos, como la capacidad de trepar por las paredes de un recipiente, o el “efecto fuente”:
Luego pueden ver un video mas reciente (en castellano) con experimentos de vórtices cuantizados en He-4 superfluido. Como vimos en clase, el hecho de que los bosones que forman el superfluido sean indistinguibles hace que los vórtices en el flujo no puedan rotar a cualquier velocidad, y que su circulación se cuantice. Las lineas blancas sobre fondo negro que se ven en los primeros 5 segundos del video son vórtices cuantizados observados en el laboratorio:
Para los que quieran leer mas sobre He-4 superfluido, les aconsejo leer el siguiente trabajo de Richard Feynman. Aunque es un poco antiguo y la interpretación actual de los rotones es diferente a la planteada en el artículo, muchas de las especulaciones que hace Feynman fueron mas tarde confirmadas en experimentos:
Este trabajo tiene una historia interesante atrás. Feynman presentó, antes de escribir el artículo, sus resultados en un congreso al que asistió Lars Onsager (que era famoso en el área). Feynman estaba bastante orgulloso de si mismo (por estos resultados, pero también se encontraba en ese estado la mayor parte del tiempo), y Onsager decidió darle una lección. La narración completa la pueden encontrar en “Surely You’re Joking, Mr. Feynman!“, pero en palabras de Feynman es más o menos así:
“Bueno, Feynman”, dijo Onsager con voz ronca, “escuché que crees que has entendido el helio líquido”.
“Bueno, sí…”
“Umm…” ¡Y eso fue todo lo que me dijo durante toda la cena! No fue muy estimulante.
Al día siguiente di mi charla, y expliqué todo sobre el helio líquido. Al final, mencioné que había algo que todavía no había logrado entender: si la transición entre una fase y la otra del helio líquido era de primer orden (como cuando un sólido se derrite o un líquido hierve, y la temperatura se mantiene constante) o de segundo orden (como ocurre en el magnetismo, donde la temperatura puede cambiar).
Entonces el profesor Onsager se levantó y dijo duramente: “Bueno, el profesor Feynman es nuevo en nuestra área, y creo que necesita ser educado. Hay algo que tiene que aprender y que debemos decirle”.
Pensé: “¡Oh no! ¿Qué hice mal?”
Onsager dijo: “Deberíamos decirle a Feynman que nadie ha podido obtener el orden de una transición a partir de primeros principios, por lo que el hecho de que su teoría no le permita calcular eso no significa que no haya entendido todo los otros aspectos del helio líquido satisfactoriamente”. Resultó ser un cumplido, pero por la forma en que comenzó, ¡pensé que me iba a dar una paliza!
Aunque Onsager probablemente nos daría una paliza, en nuestro grupo de investigación trabajamos (entre otros temas) en el estudio de flujos y turbulencia en superfluidos y en condensados de Bose-Einstein. En los dos primeros links pueden ver algunas imágenes y videos de simulaciones que hicimos de vórtices cuantizados. Para los mas curiosos (o valientes), en el tercer link les dejo un paper que publicamos hace unos años sobre viscosidad en superfluidos a temperatura finita; el paper usa muchas herramientas de la materia como el ensamble gran-canónico, el potencial químico, fonones y relaciones de dispersión, y teoría cinética y camino libre medio:
Se acabó la fiesta de los fermiones [actualizado]
Ya empieza el guateque de los bosones. [Aquí] pueden bajar la Guía 6 [actualizada el 31/5].
Eres Arnold y no lo sabes
Todos los cuerpos absorben radiación electromagnética, y emiten espontáneamente una parte en forma de radiación en equilibrio térmico con el cuerpo (es decir, como fotones a la misma temperatura que la fuente térmica). Esa es la radiación de cuerpo negro. Arnold Schwarzenegger sabe mucho sobre esto, y se cubre en barro frío cada vez que tiene que luchar contra un depredador, porque estos aliens pueden ver la radiación emitida por su cuerpo. Pero todos emitimos esta radiación, no solo Arnold (la radiación no depende de cuantas horas pasemos en el gimnasio). Así que en este post vamos a ver cómo esto se puede usar para saber qué temperatura tienen las personas en los aeropuertos, y también para saber qué temperatura tiene el universo.
¿En qué longitud de onda emite radiación de cuerpo negro una persona a 36 grados Celsius? A partir del espectro de Planck se puede ver que la máxima emisión ocurre para una longitud de onda que sigue la ley de Wien,
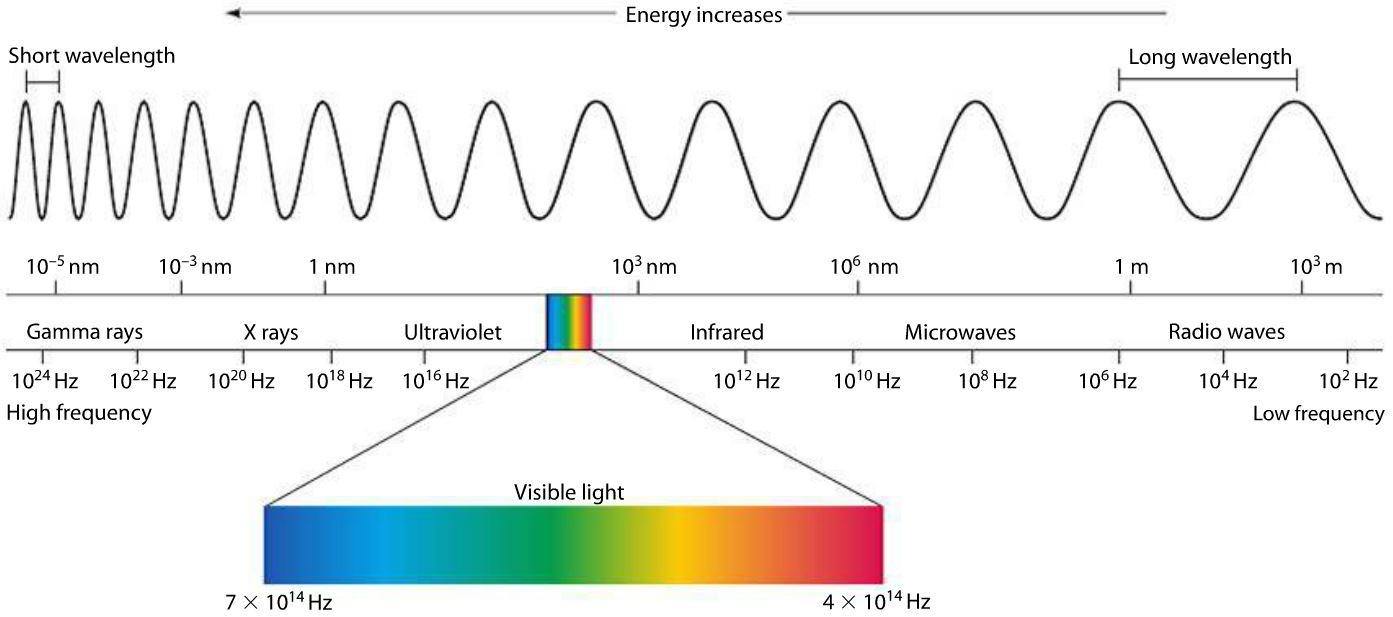
donde b = 2898 μm K. Noten que esto significa que al cambiar la temperatura del cuerpo, cambia el “color” de la radiación electromagnética emitida, ya que el color depende del espectro emitido (y fuertemente de en qué longitud de onda está el pico del espectro). Entonces ¿en qué longitud de onda debe observar una cámara para detectar este tipo de radiación? Para 36 grados Celsius, T= 309 K, y λmax ≈ 9.4 μm. De hecho, si variamos la temperatura entre 30 y 40 grados Celsius, el máximo del espectro varía respectivamente entre 9.56 y 9.26 μm (o entre 9560 y 9260 nm). Esto corresponde a radiación electromagnética infraroja. ¡Así que mirando los colores en una cámara infrarroja podemos estimar la temperatura de los cuerpos! Y así también sabemos en qué región del espectro electromagnético funcionan los ojos del depredador que persigue a Schwarzenegger:
Sabiendo esto, ¿a qué temperatura se encuentra la radiación cósmica de fondo? Estamos rodeados por radiación electromagnética de cuerpo negro que fue emitida en el momento en que se formaron los primeros átomos en el universo, y que llega a nosotros proveniente de todas las direcciones. Esta radiación corresponde a fotones que se desacoplaron de la materia en la época de recombinación: el momento en que la temperatura del universo bajó lo suficiente como para que protones y electrones pudieran combinarse formando átomos de hidrógeno (eléctricamente neutros), aproximadamente 370.000 años luego del Big Bang, y cuando el universo estaba una temperatura media de unos 3000 K. Antes, el campo electromagnético interactuaba con la materia, mientras que luego de la recombinación los fotones de la radiación cósmica de fondo dejaron de interactuar (básicamente, porque la radiación electromagnética dejó de sufrir scattering con los electrones libres). ¡Como resultado, la radiación cósmica de fondo que vemos hoy es un gas de fotones en equilibrio térmico con la materia que formaba el universo hace 13.771.700.000 años!
En 1964, Arno Penzias y Robert Wilson, realizando mediciones con una antena en los Laboratorios Bell, encontraron una extraña señal de microondas con un máximo en λmax ≈ 1 mm. Esa señal captada por la antena corresponde a este gas de fotones, mensajero del universo temprano. Usando nuevamente la ley de Wien podemos ver que esta longitud de onda corresponde a T ≈ 2.7 K (la temperatura determinada originalmente por Penzias y Wilson en 1964 era ligeramente mayor, por la incerteza experimental del instrumento). Esa temperatura corresponde a la temperatura media del gas de fotones que forma hoy la radiación cósmica de fondo. Al momento en el que la radiación se desacopló de la materia, la temperatura del gas de fotones era de 3000 K, como mencionamos antes. Pero la temperatura que medimos hoy es casi 1000 veces menor por la expansión del universo, que expandió al gas y causó una disminución de la temperatura. Porque la temperatura T de un gas de fotones cumple la ecuación que derivamos en clase,
donde U es su energía total, y V el volumen ocupado por el gas. A mayor volumen, menor temperatura.
Repulsión
[Aquí] pueden bajar las notas de la clase práctica de ayer, en donde resolvimos el problema 10 de la guía. Cosas inmediatas para hacer: resolver el problema 11 de la guía, que trata sobre el gas de Fermi-Dirac ultrarrelativista.
Una pregunta inquietante: para el gas con relación de dispersión clásica en una caja cúbica, encontramos las funciones de onda de una partícula y pudimos escribir el logaritmo de la función de partición como una suma sobre los números cuánticos nx, ny y nz. Después aproximamos la sumatoria por una integral en el impulso. Es probable que cuando resuelvan el problema 11, que trata sobre un gas ultrarrelativista, lo primero que escriban, sin reflexionar demasiado, ya sea una integral en los impulsos. Pero esa integral tiene que haber sido antes una sumatoria. Y para haber escrito esa sumatoria tienen que haber resuelto la ecuación de Schrödinger de fermiones ultrarrelativistas, si tal cosa existiera. En todo caso, tienen que haber resuelto una ecuación de onda de la cual haya resultado la cuantización de los estados para fermiones ultrarrelativistas en una caja cúbica. ¿Cuál es esa ecuación? ¿Por qué lleva a la misma cuantización para el impulso que la ecuación de Schrödinger usual?
También les quería hacer un comentario sobre el problema 9, que trata sobre un gas ideal en dos dimensiones: el ítem (c) involucra la función f1. Esta función puede escribirse en términos de funciones elementales (la integral que define a f1 puede resolverse). De ahí que sea posible escribir una expresión para el potencial químico también en términos de funciones elementales. Eso ya no será posible para el calor específico. Un ejercicio desconcertante que pueden intentar es aplicar el lema de Sommerfeld para encontrar el desarrollo del potencial químico a bajas temperaturas, tal como hicimos con el gas tridimensional, incluyendo más términos, de ser necesario. ¿Cuál es la primera contribución no nula en el desarrollo en potencias de T?
La semana que viene ya empezamos una nueva guía.
Chandra y las enanas blancas
“There’s a starman waiting in the sky,
he’d like to come and meet us
but he thinks he’d blow our minds”
David Bowie, Starman (1972).
“Chandra y las enanas blancas” no es el nombre de una banda de rock (¡podría serlo!). Pero el personaje principal de esta historia es el verdadero Starman, el hombre de las estrellas. Y los aportes que hizo a la física nos vuelan la mente. Esta es la historia de Subrahmanyan Chandrasekhar y un tipo muy particular de estrellas. Chandrasekhar ganó el premio Nobel en 1983 por sus estudios sobre la evolución y la estructura de las estrellas, pero su camino hasta ese premio no fue fácil. El Dr. Chandra, un personaje en 2001: A Space Odissey, lleva su nombre en homenaje a él.
Ayer vimos que la presión de degeneración en un gas de fermiones es central para explicar la estabilidad de estrellas enanas blancas (y también juega un rol en estrellas de neutrones). Una enana blanca es una estrella que quemó todo su material nuclear: una estrella como el Sol, luego de quemar todo el hidrógeno, quema material nuclear más pesado como el Helio. Para ello necesita mayor presión y temperatura en el núcleo, pero también genera mas energía en la reacción nuclear, y se expande hasta convertirse en una gigante roja. Luego de quemar todo el material disponible para la fusión, sufre una inestabilidad y expulsa buena parte de su masa. El núcleo de la estrella, que puede tener una masa equivalente a la del Sol pero comprimirse hasta un volumen como el de la Tierra, mantiene el calor residual y forma la enana blanca. La siguiente imágen muestra a Sirius B, una enana blanca, indicada por la flecha:
Si una enana blanca no quema más material nuclear, ¿qué mantiene a la estrella estable evitando el colapso gravitatorio? La respuesta es la presión de degeneración en un gas de Fermi: en la estrella la densidad de la materia es tan grande que el gas está degenerado (es decir, las funciones de onda de las diferentes partículas se superponen), y y la presión de Fermi es suficiente para contrarrestar la fuerza de gravedad. Recuerden que la presión de radiación resulta del principio de exclusión de Pauli. Es el hecho de que dos ferminones no puedan tener los mismos números cuánticos lo que evita que la estrella colapse gravitatoriamente. Algo parecido ocurre en estrellas inicialmente aún mas masivas, que pueden evolucionar a estrellas de neutrones. Finalmente, si la masa inicial de la estrella es aún mayor (más grande que la masa límite de Chandrasekhar), la presión de degeneración no es suficiente para evitar el colapso gravitatorio y se puede formar un agujero negro.
Los que quieran leer mas detalles sobre el balance de fuerzas en una estrella enana blanca pueden ver el siguiente link (9 páginas, en inglés):
Chandrasekhar reconoció la existencia de una masa límite, por encima de la cual las estrellas podían colapsar y formar agujeros negros, muy temprano en su carrera científica. Se enfrentó a diversos prejuicios raciales en Inglaterra y en Estados Unidos. Pero, al mismo tiempo, su idea sobre la existencia de una masa límite también se adelantó a la época. Cuando Chandrasekhar formuló su idea, el conocimiento sobre interiores estelares era bastante incipiente. Y por ese motivo muchos físicos y astrónomos presentaron dudas razonables a su validez. Chandrasekhar no bajó los brazos y a lo largo de varias décadas trabajó en mecánica estadística, dinámica de fluidos, relatividad general, y otros temas hasta crear una teoría muy sólida sobre la física de las estrellas. Mientras estudiaba estos fenómenos, y muchos otros, Chandrasekhar estableció las bases de lo que hoy conocemos como la teoría de interiores estelares, y sobre cómo evolucionan las estrellas en el tiempo. Las contribuciones de Chandrasekhar al estudio de interiores estelares, la evolución de las estrellas hasta la formación de enanas blancas o agujeros negros, y sus estudios de la estadística de Fermi-Dirac para explicar la estabilidad de las enanas blancas, lo llevaron a tener diversas disputas con astrónomos renombrados de la época, como Arthur Eddington. Y también, eventualmente, a ganar el premio Nobel junto con William Fowler.
Notas del primer parcial
Las pueden consultar [aquí], ordenadas por número de legajo según el entendimiento de Google Sheets.