Ya está disponible la guía 11 correspondiente al tema de Difracción. Esta segunda guía sobre el tema se centra sobre en la difracción causada por sistemas periódicos.
Guía 10: Difracción por un sistema simple
Ya está disponible la guía 10 correspondiente al tema de Difracción. Esta primer guía se centra sobre la difracción causada por sistemas simples.
Guía 9: Interferencia
Ya está disponible la guía 9 correspondiente al tema de Interferencia.
Guía 8: Ondas vectoriales, polarización
Ya está disponible la guía 8 correspondiente al tema de ondas vectoriales, centrada en el tema polarización.
Guía 7: ondas en mas dimensiones
Ya está disponible la guía 7 correspondiente al tema ondas en mas dimensiones.
Examen parcial
Les recuerdo que el examen parcial lo deben rendir este Viernes 9 en el aula 6 del pabellón 1 a las 17hs. Confiamos en que no les demande mucho tiempo terminarlo, por lo que les pedimos que sean puntuales. No se permiten hojas de apuntes.
Guía 5 ejercicio 8, gráfica en iPython
Les dejo acá la gráfica, y el notebook de iPython con que se generó, para que la modifiquen a gusto.
Guía 5, ejercicio 9
La excitación armónica de una cuerda tiene sus semejanzas con el efecto de tocar las cuerdas de un violín con su arco. A continuación varias observaciones empíricas en diversos artículos las cuales tendrían que poder ser explicadas por nuestros modelos.
“… any violin player will tell you that the musical pitch is not determined by the bowing speed. So what changes as you move the bow faster or more slowly? It’s the point at which the string snaps back, which is, if you think about it, the distance from the tip of the triangle to the string. Therefore, when the player moves the bow with greater velocity, the amplitude of the wave increases, but the frequency remains constant.”
“It’s possible to deduce that if the bow is one third of the distance from the bridge to the nut there can be no third, sixth, ninth, and other ‘third’ harmonics in the waveform. Similarly, a bowing position a quarter of the way from the bridge eliminates the fourth, eighth, 12th (and so on) harmonics. But if the bowing position is some arbitrary distance from the bridge, it is likely that all the harmonics will be excited to a greater or lesser degree.”
Tomado de Syntesizing Bowed Strings: the Violin family
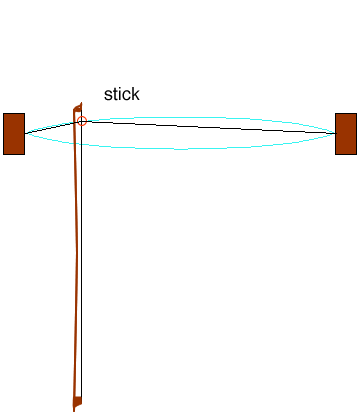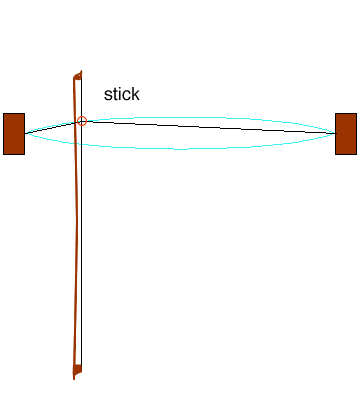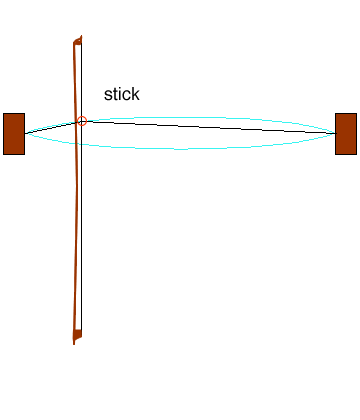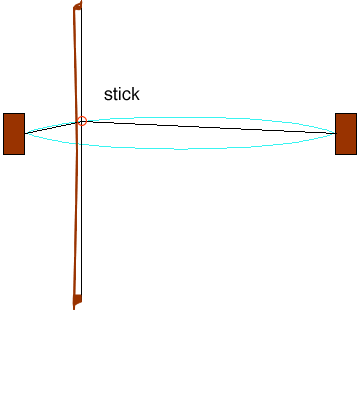
“With high static friction, the bow tends to stick to the string (“stick” in the animation) and for a while it drags the string along with it. Meanwhile, the kink in the string travels along the string and reflects at the fixed end. When the kink returns to meet the contact point, the tension in the string now acts to pull it off the bow. Under appropriate bowing conditions (that are not easy to learn!), it breaks free of the bow and then slides past it easily with very little friction, thanks to the low kinetic friction. This is the “slip” phase in the animation. The string doesn’t stop when it gets to the straight position because its momentum carries it on until eventually it stops and reverses direction. Meanwhile, the kink has travelled to the near end of the string and reflected back. At the end of the “slip” phase, it is going at about the same speed and in the same direction as the bow. At this point, it catches on the bow again, static friction reigns, and the cycle begins again.”
Tomado de Bows and Strings
Les dejo también Estos ilustrativos videos de las soluciones al problema 9 de la guía 5 fueron hechos con este código de Matllab® por Martín Caldarola. Transcribo textualmente lo que él escribo:
En todos los videos se colocó en el título el valor de frecuencia utilizado y se marca con un cuadrado de color verde la posición del forzante. Se fijaron siguientes valores para los datos del problema:
- L1 = 0.3 m.
- L2 = 0.7 m (por lo tanto L = 1 m).
- La velocidad de propagación c = 10 m/s.
- La amplitud del forzante A0 = 1 m.
Como se expuso en clase, se tiene una resonancia del lado izquierdo del forzante cuando la frecuencia es múltiplo de c/(2 L2), que en este caso resulta ser 16.67 Hz. En el video se tomó una frecuencia un poco distinta para tener una amplitud razonable, a fin de poder apreciar que la cuerda de longitud L2 se mueve de manera similar a una cuerda con extremos fijos en el primer modo y el resto de la cuerda no está en reposo.
De la misma manera se tiene una resonancia del lado derecho cuando la frecuencia es múltiplo de c/(2 L1). El video es muy similar al anterior; se observa la resonancia del otro lado y nuevamente el movimiento es similar al de la soga con extremos fijos y longitud L1.
Notar que en estos dos casos la derivada espacial en x=0 es discontinua. Recordar también la demostración realizada en la teórica, que es este problema con L1 >> L2.
Además de los mencionados casos, se tiene que la derivada espacial de función de onda resulta continua cuando la frecuencia es múltiplo de c/(2 L). Se puede apreciar que en este caso la cuerda se mueve exactamente como una cuerda de longitud L = L1 + L2, con extremos fijos en su modo fundamental (f = 5 Hz) y en el quito modo (f = 25 Hz), para dar dos ejemplos.
Ondas propagantes
Para ilustrar este concepto Martín Caldarola, un docente que “le pone mucha garra” a las prácticas, hizo el año pasado unos videos geniales. Transcribo lo él que escribió:
Les dejo acá unos videos para clarificar el concepto de onda propagante. Fueron generados en Matlab®, si alguien quiere el código está aquí.
En el video 1 se muestra una onda propagante a derecha, que se escribe como
ψ(x) = A cos(ωt − kx)
con ω = ck, donde c es la velocidad de propagación de la onda en el medio. Para el video 1 se utilizó c = 1m/s, A = 1m. El cuadrado verde está marcando la posición de un valor fijo de fase, que se mueve a velocidad c en el video, lo que evidencia la propagación de la onda hacia derecha.
En el video 2 se muestra otra onda, que se propaga a izquierda:
ψ(x) = A cos(ωt + kx)
con los mismos parámetros utilizados para el video 1. Nuevamente se marcó un valor de la fase y se sigue su posición en el tiempo con el cuadrado verde.
Por último les dejo el video del ejercicio 2 de la guía 5, que discutimos en clase el viernes pasado. Se grafica en rojo la onda incidente (es dato del problema, se propaga de izquierda a derecha):
ψinc (x) = Re {Aexp[i(ωt−kx)]} ,
y en negro la onda reflejada
ψref (x) = Re {−Aexp[i(ωt+k(x−2L))] },
donde Re{ } indica que hay que tomar la parte real.
La onda resultante es la suma de estas dos:
ψ(x) = A[cos (ωt − kx) − cos (ωt + k(x − 2L))
que se grafica en línea punteada. Nuevamente se muestran los cuadrados verdes para evidenciar la propagación de cada onda y se muestra que el punto x=L es un punto fijo. (para graficar se tomó L = 1 m.). Observación: la onda resultante es una onda estacionaria!
Guías 5 y 6
Ya están disponibles las guías de los temas ondas propagantes y de paquetes de ondas.
Estas son las últimas guías con los temas a evaluar en el primer parcial.

 Follow
Follow