Recordarán el problema 11 de la Guía 1. Eran dos partículas unidas por un resorte en caída libre en un campo gravitatorio uniforme.
Si Z es la posición relativa de las partículas y μ es la masa reducida, la evolución de Z está dada por ![]() Cuando se les pregunta en el enunciado por el rol de g en esta ecuación, la respuesta es: “ninguno”. Este resultado es general: un sistema de partículas en caída libre en un campo gravitatorio uniforme, observado desde un sistema que también está en caída libre, se comporta exactamente como si estuviera en un sistema inercial sin ningún campo gravitatorio externo. Esto sirve para hacer experimentos en gravedad cero sin tener que alejarse infinitamente de cualquier cuerpo masivo. Alcanza, por ejemplo, con construir una torre hueca muy alta, hacer vacío en su interior, construir el experimento dentro de una cápsula y dejar caer la cápsula desde lo alto de la torre. Eso es lo que hacen, con alguna variación, en la Torre de Caída de Bremen, en Alemania.
Cuando se les pregunta en el enunciado por el rol de g en esta ecuación, la respuesta es: “ninguno”. Este resultado es general: un sistema de partículas en caída libre en un campo gravitatorio uniforme, observado desde un sistema que también está en caída libre, se comporta exactamente como si estuviera en un sistema inercial sin ningún campo gravitatorio externo. Esto sirve para hacer experimentos en gravedad cero sin tener que alejarse infinitamente de cualquier cuerpo masivo. Alcanza, por ejemplo, con construir una torre hueca muy alta, hacer vacío en su interior, construir el experimento dentro de una cápsula y dejar caer la cápsula desde lo alto de la torre. Eso es lo que hacen, con alguna variación, en la Torre de Caída de Bremen, en Alemania.  Para duplicar el tiempo que pueden durar los experimentos, que de todas formas es de unos pocos segundos, en lugar de dejar caer la cápsula desde lo alto, la arrojan hacia arriba desde el fondo: también es posible subir en caída libre. [Aquí] pueden ver un interesante video (tiene subtítulos en inglés).
Para duplicar el tiempo que pueden durar los experimentos, que de todas formas es de unos pocos segundos, en lugar de dejar caer la cápsula desde lo alto, la arrojan hacia arriba desde el fondo: también es posible subir en caída libre. [Aquí] pueden ver un interesante video (tiene subtítulos en inglés).
La clase pasada vimos la precesión relativista de Mercurio, que es lo mejor que puede conseguirse en el sistema solar. En el transcurso de un siglo, las correcciones relativistas hacen que el perihelio de Mercurio avance unos 43 segundos de arco extra. Lo más asombroso, quizá, es que ese número ya se conociera, segundos de arco más, segundos de arco menos, en 1859. En el centro de la galaxia hay un agujero negro supermasivo, llamado Sagitario A*. Para algunas de las estrellas que orbitan ese agujero negro, los efectos relativistas son miles de veces mayores que para el pobre Mercurio. En el año 2020 se publicó la primera medición de la precesión de una de esas estrellas, llamada S2, con un período de revolución de 16 años. En un solo período de revolución, la precesión del periapsis de S2 es de 12 minutos de arco. La siguiente figura está tomada del artículo de la Wikipedia acerca del cúmulo de estrellas Sagitario A*, y muestra las órbitas de algunas de las estrellas.
Abajo, un video que muestra algunas de las estrellas durante 20 años de observaciones (link en la imagen a la fuente).
Otro video muy impresionante, pero completamente newtoniano, es el de cuatro exoplanetas alrededor de la estrella HR 8799.

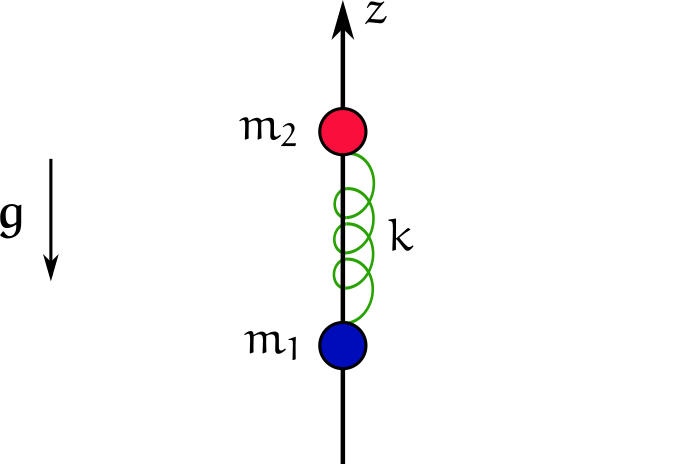
 Si siguieron el argumento del problema 13 de la Guía 2, que también pueden
Si siguieron el argumento del problema 13 de la Guía 2, que también pueden