Tal vez el principio variacional más famoso es el enunciado en el título de esta entrada, debido a no otro que a Leibniz: la realización del mundo en la que vivimos corresponde al mejor de los mundos posibles. Pero si bien este es el mejor de los mundos posibles (calculen cómo serán los otros), hay algo en lo que solemos hablar con cierta licencia cuando nos referimos a los principios variacionales en mecánica clásica, pero también en óptica, por ejemplo. El principio de Hamilton, así como el principio de Fermat, no es un principio de mínimo, ni de máximo. No se buscan los extremos de una funcional sino sus valores estacionarios.

En general, la acción para las trayectorias reales no es mínima, ni máxima. Es, simplemente, estacionaria, como son estacionarios los puntos de ensilladura en una función ordinaria, pero también sus mínimos y sus máximos. Goldstein enuncia el principio de Hamilton correctamente. En una nota a pie de página, Landau y Lifshitz tienen el reparo de aclarar que la trayectoria real puede no minimizar la acción, pero dicen que, en todo caso, extrema la acción, lo que no es cierto. Extremar significa hacer mínima o máxima. La acción sólo tiene que ser estacionaria, lo que no excluye los casos en que es mínima, pero no se restringe sólo a ellos. [Aquí] hay un paper accesible que habla del asunto. En la Guía 2, varias veces figuran las palabras extremar, extremo y extremal. Mala nuestra.

Hablando de la Guía 2, hemos subido una versión corregida. El mayor cambio está hacia el final del problema 14. El resto son detalles irrelevantes o erratas evidentes.

Libro recomendado, por lo ameno e interesante: Stories about Maxima and Minima, de V. Tikhomirov. Lo tenemos en la librería, con una gran tapa. Link en la imagen para más cosas sobre rusos y máximos. 

Para los que no pudieron venir ayer, en la teórica vieron principios variacionales. [Aquí] está la clase virtual de 2020. Al apunte lo encuentran en Material Adicional. Respecto a la práctica, ayer vimos el problema 19 de la Guía 1. [Aquí] hay una versión resuelta de 2021. No alcanza con leer el resuelto. Hagan las cuentas.

La clase que viene ya empezamos con la Guía 2. Aprovechen esta semana para avanzar lo más posible con la Guía 1. Todos los ejercicios de la guía cuentan. Si están trabados en algo, consulten en el Campus. No dejen ejercicios sin hacer.

Les dejo un breve apunte con lo que vimos ayer acerca de la función h, que no es el hamiltoniano. Es la función h. El apunte incluye la famosa demostración por el argumento de “la persona que entró al aula de casualidad”. Para bajar [aquí].

Las ecuaciones de Euler-Lagrange se deducen usualmente a partir del principio de D’Alembert: el trabajo de las fuerzas de vínculo durante un desplazamiento virtual es nulo. El propio Lagrange trató en varias ocasiones de demostrar este principio, pero sus demostraciones son vanas. La mecánica lagrangiana surge de la conjunción de las leyes de Newton y del principio de los trabajos virtuales. La mecánica lagrangiana no es una presentación nueva de las leyes de Newton.

De manera que tienen tanto derecho a sentirse incómodos con el principio de D’Alembert como a sentirse incómodos con los axiomas de Euclides o con los de la mecánica cuántica. Lo digo seriamente.

Aquí les dejo un par de citas de libros muy recomendables. Pueden hacer click en las imágenes para ampliarlas. La primera cita es de Sommerfeld (Mechanics, 1952, pp. 52-53):

En el mismo espíritu, Lanczos dice lo siguiente (The variational principles of mechanics, 1949, p. 77):

El postulado A del que habla Lanczos es el principio de D’Alembert.

La figura que encabeza esta entrada está basada en una de las demostraciones del principio de los trabajos virtuales ofrecida por Lagrange, que nunca hizo ese dibujo ni ningún otro. Para Lagrange era cuestión de honor hacer todo de manera analítica, sin el auxilio de figuras.

Todos están familiarizados con el péndulo simple que muestra la figura:

Las ecuación F = m a puede descomponerse en dos componentes, una paralela a la barra, que nos dice cuánto vale la tensión T, y otra perpendicular a la barra, que nos dice cuánto vale la aceleración angular. Esa es la ecuación de movimiento propiamente dicha, que se lee como:

Todo bien con el péndulo simple. Pero imagínense que están en Física I y que les dan el siguiente péndulo doble “fijo”:

Este péndulo tiene la particularidad de que las barras no están articuladas. El ángulo φ puede variar pero las dos barras se mantienen alineadas. Seguramente (pensarán) debe ser más sencillo que el péndulo doble usual, porque hay una sola coordenada de la que preocuparse. Entonces, siempre en el contexto de Física I, construimos los diagramas de cuerpo libre para cada partícula. Lo más natural parece ser aplicar las mismas hipótesis que usamos para construir el diagrama de cuerpo libre del péndulo simple. Les quedan las siguientes dos figuras:

La proyección de las ecuaciones de movimiento en la dirección de la barra les vuelve a dar los valores de las tensiones, que aquí importan poco. En la dirección perpendicular a la barra, las únicas fuerzas que importan son los pesos. La aceleración de la primera partícula proyectada en la dirección perpendicular a la barra es

y la de la segunda partícula es

Los pesos proyectan según el seno del ángulo, de modo que, si todo está bien, las ecuaciones de movimiento para cada partícula son

Aquí se ve que hay un problema. El ángulo no puede evolucionar al mismo tiempo según estas dos ecuaciones de movimiento. Algo hemos hecho mal. La pregunta es ¿dónde está el error? Como diría Paenza, deténganse aquí un momento y traten de pensar qué está pasando y qué cosa puede estar mal en las hipótesis que asumimos para llegar a estas dos ecuaciones contradictorias.

Veamos que nos dice la formulación lagrangiana. Las energías cinéticas son

Por otro lado, las energías potenciales están dadas por

Con esto, el lagrangiano resulta:

La ecuación de movimiento es

Recién estamos conociendo al formalismo lagrangiano, pero confiamos en que esta ecuación es la correcta. Es posible analizar varios límites. Por ejemplo, l₂ = 0, m₁ = 0. Todo parece andar bien.

Para terminar de convencernos de que la ecuación anterior es correcta, hay otra manera de deducirla con métodos de Física I, a partir de la ecuación para la variación del momento angular en términos de los torques. Después de todo, este sistema es lo que llamaríamos un péndulo físico. Deberían poder verificarlo rápidamente y así convencerse de que la ecuación anterior es la correcta.

Saber que la ecuación está bien no resuelve el misterio de por qué las otras dos ecuaciones estaban mal. La pregunta persiste: ¿por qué está mal el primer procedimiento? Un camino para llegar a la respuesta es usar la ecuación de movimiento correcta para encontrar las fuerzas de vínculo sobre cada partícula. No es difícil y la solución es bastante esclarecedora, así que les recomiendo que lo hagan. Hay un punto clave que es mejor dejar que ustedes descubran.

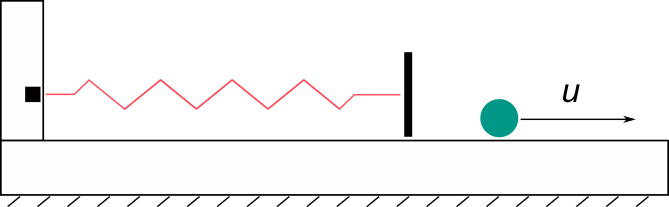
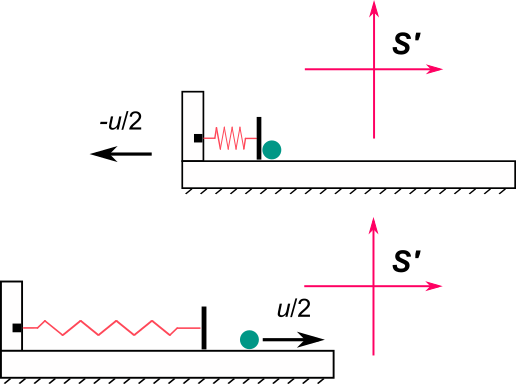
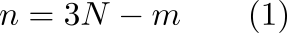La ecuación más inútil del mundo es la que dice que si tienen un sistema de N partículas, sometidas a m vínculos independientes, entonces el número de coordenadas generalizadas necesarias para describir la configuración del sistema es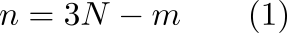Esta ecuación ejerce una especie de fascinación en el neófito, pero su utilidad práctica es nula. Hay otras ecuaciones parecidas en la física y en la matemática que relacionan números enteros. Por ejemplo, la regla de las fases de Gibbs o la fórmula de Euler para los poliedros. Esas ecuaciones sí son muy útiles. La ecuación (1) es más una definición del número de vínculos en términos del número de coordenadas generalizadas, que una definición del número de coordenadas generalizadas en términos del número de vínculos.

La prueba de que el número de coordenadas generalizadas es n debe evitar el uso de la ecuación anterior. Debe ser una prueba constructiva: tienen que definir las  n coordenadas generalizadas, mostrar explícitamente que las posiciones de las N partículas se pueden escribir en términos de esas coordenadas y que, además, se cumplen todos los vínculos.

¿Cuál es el problema con la ecuación n = 3N – m? El problema es que la definición de vínculo es muy vaga. Con frecuencia, al nivel más bajo de rigor, directamente se asocia un vínculo a un enunciado. Por ejemplo, los enunciados “la distancia entre las partículas 1 y 2 vale L“, o ”la partícula 1 se mueve sobre una esfera”, se cuentan (correctamente) como un vínculo. Pero si dijera “la partícula 1 se mueve sobre un círculo”, ese enunciado representa en realidad dos vínculos: “la partícula 1 se mueve sobre un plano” y “la partícula 1 se mueve sobre una esfera (cuya intersección con el plano es no vacía)“. De manera que asimilar vínculos con enunciados informales de las condiciones no es el camino adecuado para averiguar cuántas coordenadas generalizadas van a necesitar para describir un sistema.

Como caso extremo, consideren una partícula que se mueve en el plano. Sin vínculos adicionales, se necesitarían dos coordenadas.  Impongan entonces la condición “la suma de las distancias de la partícula a los tres lados de cierto triángulo equilátero de altura L es L“. Cualquier punto interior al triángulo satisface la condición, de manera que lo único que dice la condición anterior es que la partícula se mueve en el interior del triángulo. Ninguna coordenada ha sido eliminada. Sin embargo, esta condición no es en apariencia muy distinta a esta otra: “la suma de las distancias de la partícula a dos puntos separados una distancia L es L“. Es fácil ver que la partícula debe moverse sobre el segmento que une los dos puntos, de modo que el número de coordenadas se ha reducido en una unidad. 

Condiciones en apariencia similares, tienen consecuencias muy distintas sobre el número de coordenadas generalizadas.

Para dar más precisión a la ecuación (1), lo usual es representar al vínculo como una ecuación que liga las posiciones de las partículas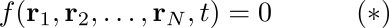Entonces se razona que si existe una ecuación que involucra a las 3N coordenadas, debe ser posible eliminar una de esas coordenadas. Por cada ecuación (sigue el razonamiento) se elimina una coordenada; si hay m ecuaciones, al final de todo se habrán eliminado m coordenadas, y el número necesario de coordenadas para especificar la configuración del sistema será 3N - m. 

Ahora bien, ¿por qué una ecuación de la forma (∗) permitiría eliminar una coordenada en términos de las otras? En el ejemplo que vimos antes de la partícula dentro del triángulo, la condición “la suma de las distancias a los lados del triángulo es L” puede formalizarse como: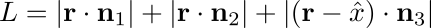

Aquí estamos suponiendo que el triángulo tiene un vértice en el origen, un  lado sobre el semieje x positivo y que las normales interiores a los tres lados son los versores n_i. No es inmediato (pero en realidad es muy simple) ver que, para cualquier punto interior al triángulo, la ecuación anterior es una identidad, de modo que no representa ninguna condición de vínculo. Una ecuación, cero vínculos.

Tenemos así un caso en que una ecuación no reduce el número de coordenadas. En el otro extremo, podemos escribir una ecuación que reduce a cero el número de coordenadas: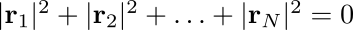

Es una sola ecuación, pero implica que las 3N coordenadas cartesianas tienen que ser iguales a cero. Una ecuación, 3N vínculos.

Siempre pueden aplicar este truco para expresar como una sola ecuación m ecuaciones de vínculo. Supónganse que sus ecuaciones de vínculo son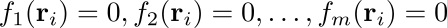

Estas m ecuaciones son equivalentes a esta sola ecuación: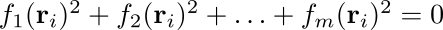

De modo que no hay ninguna correspondencia entre el número de ecuaciones y el número de coordenadas que pueden eliminarse a partir de esas ecuaciones. Decir, “tengo tantas partículas y tantas ecuaciones de vínculo, por lo tanto tengo tantas coordenadas generalizadas” no está, en general, justificado. Para que eso sea cierto, las ecuaciones tienen que ser de un tipo especial: tienen que definir hipersuperficies de dimensión 3N - 1. Si no van a acompañar la ecuación (1) de una demostración de que las ecuaciones de vínculo son de ese tipo, entonces mejor no usar la ecuación (1).

Lo repito: en lo que respecta a los problemas de la práctica, la prueba de que necesitan n coordenadas para especificar la configuración de un sistema debe ser constructiva. Deben definir claramente las coordenadas y mostrar de manera explícita que pueden escribir las posiciones de todas las partículas usando esas coordenadas. Eso es, en definitiva, lo importante, y no saber cuál es el número de coordenadas generalizadas.

Este lunes 20 de marzo a las 17 horas empieza el curso de Mecánica Clásica del primer cuatrimestre de 2023. ¿En qué aula? Nadie lo sabe. Lo que sí sabemos es que vamos a necesitar un aula más grande. Tenemos más de 115 inscriptos.

Les aconsejamos que se suscriban a la página de la materia y también que se matriculen en el campus. Las noticias las daremos a través de la página. El campus está principalmente para que puedan hacer consultas en cualquier momento.

El cronograma de la materia ya está publicado, incluidas las fechas de los parciales. Tomen nota y no permitan que otras cátedras reclamen la prioridad. También están publicadas las primeras dos guías. Los que vengan de cursos anteriores notarán que las guías cambiaron. Recursantes o primerizos, no es mala idea que intenten estar un paso adelante de la práctica; por ejemplo, empezando a resolver desde ahora los problemas de la guía de repaso. Sólo hay una clase reservada para esta guía. La segunda clase ya empezamos con la formulación lagrangiana. Lo que sí es una mala idea es que se retrasen con las guías. En el primer parcial entran muchos temas, pero por suerte ya han visto algo de fuerzas centrales y de pequeñas oscilaciones.

Miren la bibliografía, bajen los libros y vayan conociéndolos. Una lectura siempre recomendable son las entretenidas notas bibliográficas de la segunda edición del libro de Goldstein.

Como dice Landau, ya sin más, esperamos verlos el lunes.