Hechos inquietantes 10

Posted on by

En el problema 15 de la Guía 7, se pide demostrar que, para una partícula, si se conservan dos componentes del momento angular, entonces se conserva la tercera. La indicación de que se trata de una partícula sirve para fijar la definición de L,

Por componentes, se entiende que se trata de las componentes cartesianas. La demostración es una aplicación muy sencilla de la identidad de Jacobi y del hecho de que el corchete de dos componentes distintas de L es, quizá a menos de un signo, igual a la tercera.

Ahora bien, consideren una partícula en caída libre en un campo gravitatorio uniforme, como muestra la figura. La partícula viaja a lo largo de la recta x = x0, y = 0.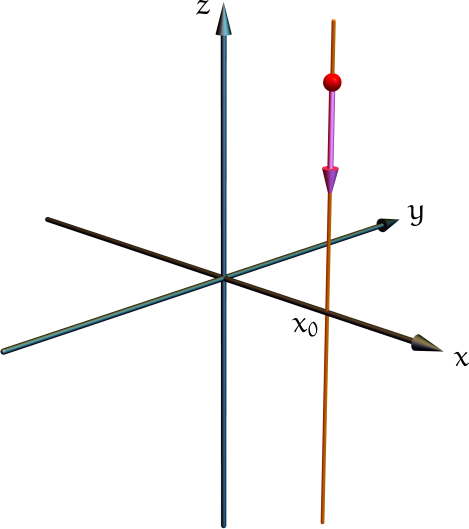 

Su posición en función del tiempo es

Su velocidad esLuego, su momento angular resulta

Ocurre entonces que dos componentes de L se conservan,

pero la tercera no se conserva,

¿Dónde está la trampa?

Guía 8

Posted on by

La remozada Guía 8 puede bajarse [aquí]. Por remozada queremos decir que le cambiamos el tipo de letra. Con el tipo de letra, también le cambiamos las letras. Y con las letras, los problemas. Contiene una sola integral terrible. Bueno, dos.

Guía 6. Problema 22.

Posted on by

Esto es lo que hace el giróscopo del problema 22 de la Guía 6.
No sólo las condiciones iniciales están elegidas para que el problema pueda integrarse en términos de funciones elementales, sino que la solución es fácil de interpretar. Deberían ver en sus soluciones que el giróscopo hace lo que muestra la animación anterior. El problema 22 guarda una gran analogía con el problema 19.

Una cuestión interesante es de dónde viene el giróscopo para llegar a esa condición inicial. Si propagamos la solución hacia los tiempos negativos, vemos que el giróscopo viene de la misma posición asintótica hacia la que tiende en el futuro. Abajo hay una animación entre -T y T, con T suficientemente grande para ver el comportamiento asintótico hacia el pasado y hacia el futuro.

Hechos inquietantes 9

Posted on by

Supongan que tienen un sistema cuyo lagrangiano es igual a la energía cinética,
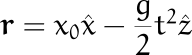
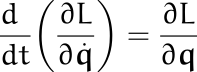
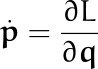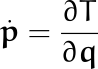
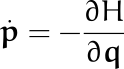
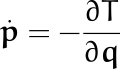Puede ser, por ejemplo, una partícula libre en coordenadas esféricas, para que no sea tan trivial; o una partícula que se mueve sobre una superficie, sometida sólo a la fuerza de vínculo. En general, las ecuaciones de Euler-Lagrange sonUsando la definición del momento conjugado, esto también puede escribirse comoPara el caso específico que estamos analizando, quedaPor ejemplo, en el caso de la partícula libre en coordenadas esféricasy una de las ecuaciones esque claramente no tiene por qué ser cero, aunque la partícula sea libre. Hasta aquí todo parece en orden. Los problemas surgen cuando intentamos comparar las ecuaciones de movimiento del formalismo lagrangiano con las del formalismo hamiltoniano.

Asumiendo que T es una función homogénea de grado 2 en las velocidades, el hamiltoniano de este problema es simplemente

En general, la ecuación de Hamilton para los impulsos conjugados es

En el caso específico que estamos considerando, resultaPero esta ecuación tiene justo el signo contrario de la que escribimos anteriormente

Ya vimos con un ejemplo que, en general, la derivada de p no es cero. Entonces, ¿cuál es la ecuación correcta?

Hechos inquietantes 8

Posted on by

De manera que tenemos un cuerpo rígido en forma de prisma cuadrado puesto simétricamente sobre el filo de un semiplano. El cuerpo no es homogéneo, sino que tiene un peso sobre uno de sus bordes, como muestra la figura.
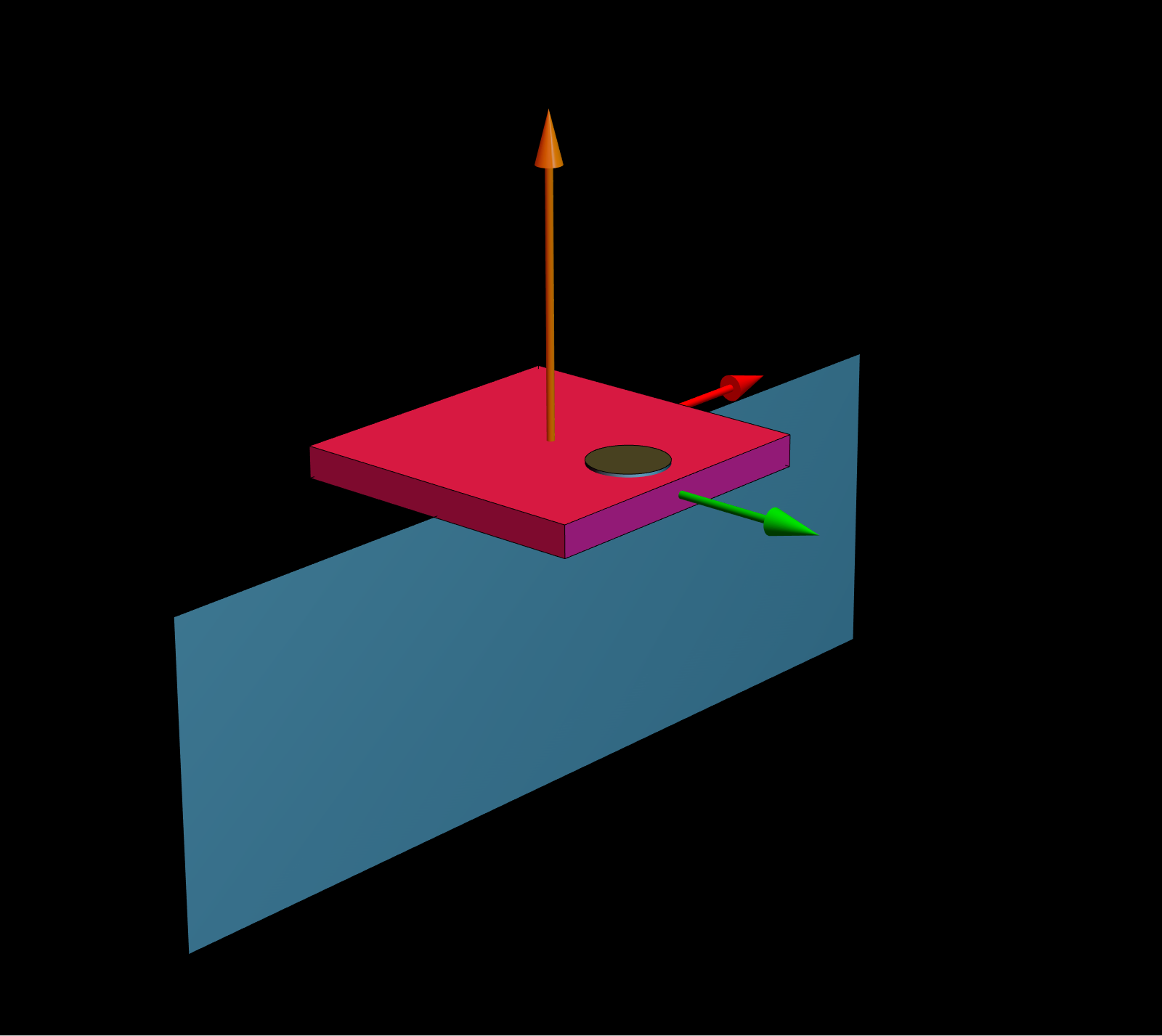Inicialmente los ejes del cuerpo coinciden con los ejes xyz. Todos los ángulos de Euler son cero. Demostrar que el cuerpo permanece inmóvil.

Inestabilidad del eje intermedio

Posted on by

Abajo hay un video que muestra la inestabilidad del eje intermedio en la Estación Espacial Internacional. Link en la imagen.

En la guía sólo se pide demostrar la estabilidad o la inestabilidad. Pero el movimiento puede determinarse exactamente por cuadraturas usando cierta clase de funciones. Está hecho en la sección 37 del libro de Landau y Lifshitz. [Aquí] hay un paper más detallado. En [este] video está explicado más gráficamente y a nivel del público general. Ahí se plantea la siguiente pregunta inquietante: ¿podría estar la Tierra rotando alrededor del eje intermedio y en cualquier momento quedamos todos patas para arriba? En el video está dicho de manera más técnica. Goldstein menciona el problema en el contexto de los satélites artificiales, en la sección 5-6, en una nota a pie de página que empieza como “If there are dissipative mechanisms present, these stability arguments have to be modified…” Al menos en mis ediciones, está en la página 210 de la segunda y en la 205 de la tercera. En la versión en español, la nota empieza diciendo “Cuando haya mecanismos disipativos, habrá que modificar estos razonamientos acerca de la estabilidad”, y está en la página 267. Ya lo he dicho antes: es muy buena la versión del libro de Goldstein en español.

En el post anterior, en el minuto 6:40 del video, se ve un trompo que se da vuelta. Es el ["Tippe top"]. Al contrario del fenómeno del eje intermedio, el comportamiento de este trompo depende de que haya torques externos. Abajo, una fotografía muy famosa de Pauli y Bohr jugando con un Tippe top.

Hechos inquietantes 7

Posted on by

Un día en Mercurio dura dos años, de los de Mercurio, no de los de la Tierra. Link en la imagen. Cuando la flecha apunta al Sol, en ese punto de Mercurio es mediodía. Cuenten cuántas revoluciones da Mercurio entre dos mediodías sucesivos.

Tecnicismos

Posted on by

Técnicamente, como aún no son las 22,  todavía estamos en clase. Les dejo un breve apunte que sigue más o menos lo que hicimos durante la clase de hoy. Lo pueden bajar [aquí]. Con lo que han visto, pueden resolver casi todas las cuestiones del problema 1 y hacer (en parte rehacer) los problemas del 6 al 10. Empiecen con el pie derecho y no se atrasen con los problemas. Consulten ahora y no en el parcial.