Esta semana no habrá teóricas, pero sí prácticas. Y para los que se perdieron la teórica del miércoles pasado, hago acá un breve resumen.
El miércoles empezamos a estudiar la ecuación de Kuramoto-Sivashinsky. Estos son los apuntes de la clase:
También mostré un Colab que resuelve esta ecuación con condiciones de contorno periódicas, usando las siguientes condiciones iniciales:
La ecuación de Kuramoto-Sivashinsky sufre una serie de bifurcaciones a medida que se aumenta el tamaño del dominio L (aumentar L es equivalente a disminuir la disipación en el sistema, haciendo al término no lineal y al término de reacción más relevantes). Y para L suficientemente grande, la ecuación desarrolla caos espacio-temporal.
Aquí pueden ver en un mapa de colores la evolución de u(x,t) para L = 4π. Noten que el sistema evoluciona a una solución suave y con pocos modos espaciales excitados:
Para L = 12π la solución es:
Para L = 30π, la solución es:
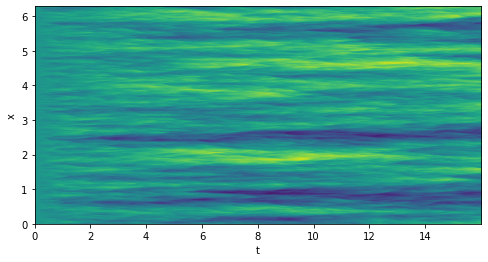
Para L = 60π:
Y finalmente, para L = 120π:
Las soluciones de esta ecuación para L grande tienen propiedades fractales. Cuando nos volvamos a ver en la teórica, veremos cómo caracterizar estas bifurcaciones, y cómo estudiar los patrones espacio-temporales en el sistema.