Acá Juan nos deja una buena explicación de cómo se encara y resuelve el ejercicio 8 de la guía 5: link

Les dejo la resolución del ejercicio del Landau de la guía 5: link

El lunes a las 16 hs todos aquellos que fueron a la Reunión de la AFA pueden pasar por mi oficina para hacer un repaso de una hora de los temas que vimos durante la última semana. Es muy probable que el repaso lo hagamos en la pecera grande frente a mi oficina. ¡Sean puntuales!

A pedido del público, aviso también que este lunes no habrá teórica, para que puedan hacer consultas desde las 17 hs. Aprovechen para sacarse todas sus dudas, luego del parcial retomamos el dictado habitual del curso.

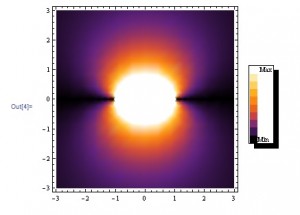
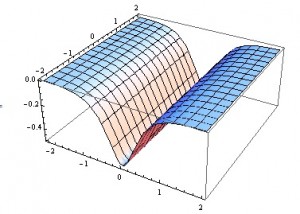
La clase pasada vimos un problema donde combinamos varios conceptos. Por un lado, el método de Green de Dirichlet cuando conocemos el potencial en el borde. Por otro lado, cómo extender analíticamente una solución que conocemos en el eje. Y por último, como quedan las series de Bessel cuando el espacio en $\rho$ no está acotado. Aquí les dejo un file de mathematica analizando las soluciones que habíamos obtenido: link

Para los interesados, les dejo un file de Mathematica donde analizo las soluciones que obtuvimos en el problema 4 de la guía 2: acá.

Desde el lunes 2 de septiembre y hasta el domingo 8 de septiembre estará abierta nuevamente la inscripción a la materia en el sistema SIU Guaraní de la facultad. Los que no se hayan inscripto en la materia, o hayan tenido algún problema con su inscripción, pueden aprovechar estas fechas para completar la inscripción. Y tengan en cuenta que esta es la última oportunidad: si no se inscriben ahora, van a tener que cursar Física Teórica 1 en el Universo 6.

En otro curso un alumno me preguntó si las series de Fourier que quedan en problemas tipo cajas convergen rápidamente, pues él hizo el intento con uno de los problemas de la guía y no veía la convergencia. En el archivo de Mathematica que les dejo a continuación, veo el caso de una caja con una sola tapa a un potencial fijo y las otras 5 tapas a tierra. Como pueden ver y jugar en el archivo las series convergen muy rápido. Para el interesado: acá

Este video lo pongo en todas las páginas de los cursos que dicto. Lo mencioné brevemente en clase hace una semana, y llegó el momento de ponerlo aquí para que todos los que no lo vieron antes, lo vean (y los que ya lo vieron pueden volver a verlo, porque siempre se puede volver a ver a Feynman).

El video muestra una clase brillante de Richard Feynman explicando su visión sobre como se construye una teoría. Alcanza con mirar el primer minuto:

En el video Feynman dice que la búsqueda de una nueva ley comienza “adivinándola” (“first, we guess it“). Luego se derivan consecuencias y predicciones a partir de esa ley “adivinada”, y se verifican (o no) esas predicciones con experimentos. Y a continuación Feynman es categórico: “If it disagrees with experiments, it’s wrong. And that simple statement is the key to science. It doesn’t make a difference how beautiful your guess is, it doesn’t make a difference how smart you are, or who made the guess or what his name is, if it disagrees with experiments… it’s wrong.”.

El video luego continúa con Feynman hablando de platos voladores, pseudociencias, y conceptos del método científico. Si tienen tiempo, les aconsejo mirarlo completo.

Esta es la foto del pizarrón de Richard Feynman el día de su muerte. La frase mas citada es “What I cannot create I do not understand”, pero la que nos va a interesar como motivación para la materia es la que aparece abajo: “Know how to solve every problem that has been solved”, o

Saber cómo resolver cada problema que ha sido resuelto.

A la derecha pueden ver una lista de problemas a estudiar (“To learn”). Esa lista incluye al ansatz de Bethe (un método para encontrar soluciones exactas a un modelo simplificado de materiales antiferromagnéticos), el efecto Kondo (el cambio en la resistividad eléctrica de un metal por el scattering de los electrones en impurezas magnéticas), el efecto Hall en dos dimensiones, e hidrodinámica clásica no-lineal, entre otros. Uno de estos problemas (Kondo) aparece tachado, probablemente porque Feynman consideró que ya había comprendido suficientemente bien el tema.

Hablando de pizarrones, no quiero ser pájaro de mal agüero pero la imágen que aparece mas abajo podría ser premonitoria de la clase del miércoles.