Con Ricardo estudiaron en la última clase teórica el problema de un fluido viscoso en contacto con una placa plana, la cual es puesta en movimiento súbitamente con una velocidad constante paralela al plano de la misma. Esta situación física corresponde al problema 8 de la Guia de fluidos viscosos.
Me pareció interesante dejarles aquí un video del experimento realizado en el laboratorio empleando un fluido viscoso (newtoniano). El fluido en este caso es un aceite siliconado translúcido (polydimethylsiloxane) de parámetros reológicos conocidos (densidad y viscosidad). El video muestra una vista superior de un recipiente lleno de este fluido, una de cuyas paredes es móvil (borde inferior en el video). El fluido ha sido marcado con un trazador (colorante azul), sobre una línea perpendicular al plano de la pared móvil.
Cuando la pared en contacto con el fluido (inicialmente en reposo) se mueve repentinamente, las capas de fluido cercanas a la misma son arrastradas con la pared, producto del esfuerzo viscoso en la interfaz. Las regiones de fluido más distantes o bien se mueven a una velocidad menor, o bien permanecen quietas. Observen y podrán notar (gracias a la presencia del trazador) que existe una capa (de determinado espesor) cerca de la placa donde las fuerzas viscosas ya han tenido un efecto y otra región en donde sus consecuencias aún no se han sentido.
Pregunta: El ancho de dicha capa, cómo escala con el tiempo?
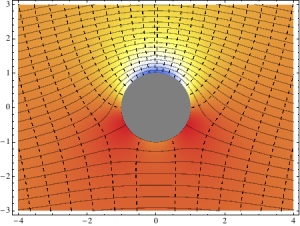
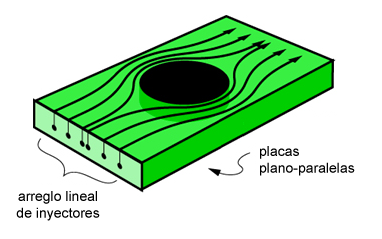La figura muestra un esquema simple de una celda de Hele-Shaw, ilustrando el flujo en torno de un obstáculo; un arreglo lineal para la inyección de colorante (como trazador) y algunas líneas de corriente a modo de visualización. El flujo dentro de la celda, laminar y paralelo, se conoce como flujo de Poiseuille plano y será objeto de estudio en la segunda mitad de la materia (en el marco de la guía de flujos viscosos).
