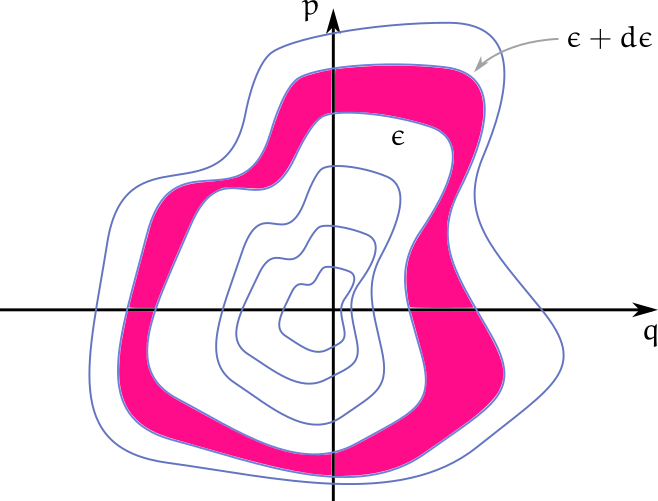
Caben muchos bosones en el estado fundamental. Ayer fue San Cono, lo que nos toca de cerca como físicos. Ayer también resolvimos en la práctica un problema fuera de guía, pero asiduo en los parciales: el problema del gas de bosones en una caja con gravedad. ¿Hay condensado? ¿No hay condensado? ¿Cuál es su aplicación en la reparación de relojes y, por qué no, en la relojería? Cuántas preguntas. [Aquí] pueden bajar el guion original de la clase de ayer. Trae extras. El ítem (d) es para medir fuerzas.

Quedó pendiente una versión 2024 1c de las notas de clase sobre condensados en una trampa armónica. Les dejo el apunte de la clase del cuatrimestre pasado, [aquí]. Pero también la serie de gráficos que mostramos durante la clase de la semana pasada, [aquí]. Son mucho mejores que los del apunte. Si estos gráficos no los convencen de que el nivel fundamental es el único que hay que separar al hacer la aproximación de sumas por integrales, entonces no sé cómo persuadirlos.

El problema del condensado en una trampa armónica nos sirvió de excusa para presentar la llamada aproximación semiclásica, que permite pasar de sumas sobre estados cuánticos a integrales en el espacio de fase clásico, sin necesidad de resolver la ecuación de Schrödinger. Llegamos a verlo en la clase de la trampa armónica, donde el espectro cuántico de energías es sencillo, y también lo vimos ayer en el problema del gas en la caja con gravedad, donde el espectro de energías es un horror. Me pareció oportuno escribir un apunte con las n maneras de aproximar por integrales la suma sobre estados para el caso de la trampa armónica, una de las cuales es la aproximación semiclásica. Pueden bajar el flamante apunte [aquí]. Incluye un apartado especial para los fundamentalistas de la densidad de estados. Algunas imágenes pueden producir convulsiones.

[Aquí] pueden bajar una versión taquigrafiada de la clase práctica del lunes, en donde resolvimos el problema 1 de la Guía 6. El ítem respecto a la presión necesitaba revisarse; pueden bajar la versión actualizada de la guía [aquí]. Al final de las notas hay algunos problemas propuestos.

La parte central del problema 1 es razonar la transición de fase. Ahora bien, una vez que lo entendieron, no es necesario aplicar paso por paso los mismos razonamientos a todo problema de condensación de Bose-Einstein que se les presente. No necesitan inventar continuamente la rueda. Lo digo porque en los parciales suelen hacer eso. La rueda ya la damos por inventada, vayan directamente al asunto.

La condensación de Bose-Einstein tiene al menos dos puntos inciertos: el primero es la prescripción de separar en las sumas el término del nivel fundamental y aproximar el resto por una integral. El segundo es entender por qué hay una transición de fase y cómo toda la cuestión depende de manera decisiva de que se tome el límite termodinámico. Este segundo punto está explicado en el apunte de manera bastante formal, a diferencia de la mayoría de los argumentos que encontrarán en los libros. A primera vista, estos argumentos parecen suficientes, pero si se vieran en la necesidad de explicárselos a alguien, descubrirían, con gran azoramiento, que no son tan convincentes como creyeron. Como si repitieran en público un chiste y comprendiesen, cuando ya es demasiado tarde, que sólo lo recuerdan imperfectamente.

Respecto a la prescripción que indica separar la contribución del nivel fundamental y aproximar el resto por una integral, no tengo más que decir que es, como escribiría Lovecraft, intelectualmente repugnante.

En el único, único libro en donde he visto demostrado que esto tiene rigor matemático es en el de Pathria y Beale, en su apéndice F. Hasta cierto punto se entiende todo, pero después entra a jugar el resultado de un paper y la cosa se complica. Pero la demostración existe.

La prescripción de separar e integrar es difícil de justificar gráficamente para el caso del gas en una caja, porque se trata de una integral triple. Para el gas en una trampa armónica, uno puede transformar la suma triple en una suma simple. Como vimos el miércoles, entonces es evidente que la prescripción de separar e integrar es del todo razonable y justificada. El apunte sobre la clase del miércoles está en preparación. Mientras tanto, los urjo a leer las secciones sobre condensado en una trampa armónica en la edición de 2021 del libro de Pathria y Beale, aunque sólo el primero de ellos sea poeta urdu.

Ya empieza el guateque de los bosones. [Aquí] pueden bajar la Guía 6 [actualizada el 31/5].

[Aquí] pueden bajar las notas de la clase práctica de ayer, en donde resolvimos el problema 10 de la guía. Cosas inmediatas para hacer: resolver el problema 11 de la guía, que trata sobre el gas de Fermi-Dirac ultrarrelativista.

Una pregunta inquietante: para el gas con relación de dispersión clásica en una caja cúbica, encontramos las funciones de onda de una partícula y pudimos escribir el logaritmo de la función de partición como una suma sobre los números cuánticos n_x, n_y y n_z. Después aproximamos la sumatoria por una integral en el impulso. Es probable que cuando resuelvan el problema 11, que trata sobre un gas ultrarrelativista, lo primero que escriban, sin reflexionar demasiado, ya sea una integral en los impulsos. Pero esa integral tiene que haber sido antes una sumatoria. Y para haber escrito esa sumatoria tienen que haber resuelto la ecuación de Schrödinger de fermiones ultrarrelativistas, si tal cosa existiera. En todo caso, tienen que haber resuelto una ecuación de onda de la cual haya resultado la cuantización de los estados para fermiones ultrarrelativistas en una caja cúbica. ¿Cuál es esa ecuación? ¿Por qué lleva a la misma cuantización para el impulso que la ecuación de Schrödinger usual?

También les quería hacer un comentario sobre el problema 9, que trata sobre un gas ideal en dos dimensiones:  el ítem (c) involucra la función f₁. Esta función puede escribirse en términos de funciones elementales (la integral que define a f₁ puede resolverse). De ahí que sea posible escribir una expresión para el potencial químico también en términos de funciones elementales. Eso ya no será posible para el calor específico. Un ejercicio desconcertante que pueden intentar es aplicar el lema de Sommerfeld para encontrar el desarrollo del potencial químico a bajas temperaturas, tal como hicimos con el gas tridimensional, incluyendo más términos, de ser necesario. ¿Cuál es la primera contribución no nula en el desarrollo en potencias de  T?

La semana que viene ya empezamos una nueva guía.

Las pueden consultar [aquí], ordenadas por número de legajo según el entendimiento de Google Sheets.

Ahora que tengo su atención, voy a hablar de las notas del parcial. Van a estar publicadas hoy alrededor de las 16:40 19 horas. Traten de estar en el aula a eso de las 16:50, para que les devolvamos los parciales. Dejamos para el miércoles las consultas sobre la corrección.

• Primero: hay una versión notoriamente distinta del apunte acerca del problema 3 de la Guía 5, que trata sobre la función de partición canónica de N partículas idénticas no interactuantes. [Aquí].
• Segundo: lecturas recomendadas para el cálculo de la masa de Chandrasekhar: el libro de Pathria y Beale y el libro de Huang. [Aquí] pueden bajar un apunte de clase, preparado el cuatrimestre pasado, pero inédito.
• Por último: pueden leer sobre paramagnetismo de Pauli en casi cualquiera de los libros de la bibliografía. Pathria y Beale despachan rápidamente el resultado a temperatura cero y luego discuten el caso general y el de bajas temperaturas. [Aquí] pueden bajar un apunte de cursos pretéritos.
• Finalmente: es probable que las notas de los parciales estén el lunes.

Los problemas de la Guía 5 que vimos hoy en la clase de práctica están pasados en limpio en los siguientes apuntes del cuatrimestre pasado (la numeración puede diferir):

• Problema 1: paso de sumas a integrales para la función de partición canónica de una partícula en una caja.
• Problema 3 [versión actualizada]: expansión en potencias del volumen de la función de partición canónica para N partículas indistinguibles en una caja. El límite clásico y la justificación del conteo no tan correcto de Boltzmann.
• No exactamente el problema 4, pero relacionado. Función de partición gran canónica, funciones de Fermi-Dirac y más cosas que veremos en las próximas clases.

El ensamble virtuoso

Radu Balescu, “Equilibrium and Nonequilibrium Statistical Mechanics”.

La explicación más razonable I

Richard Feynman, Nobel Lecture.

La explicación más razonable II

Arthur Schopenhauer, citado por Borges en “Otras Inquisiciones”.

Un doble

Edgar Allan Poe, William Wilson.

La Guía 5 puede bajarse [aquí].

Actualización: esta semana sólo hay clases prácticas, de 17 a 22.

[Aquí], el primer parcial. [Aquí], las soluciones.

Hoy, alguien se olvidó una calculadora. El lunes pasado, en el aula quedó una lapicera tuneada.