Ahora que he malhecho su atención con un título burlesco y un verbo de dudosa existencia, permítanme aclararles que lo que vine a decirles no está relacionado directamente con el parcial, salvo que es a las 10:30 en el aula de clases. Lo que sigue es para completar la clase del jueves pasado. En esa clase encontramos la transformación a las variables de ángulo-acción para un pozo cuadrado de potencial en una dimensión, es decir, una partícula rebotando entre dos paredes. Como el movimiento es esencialmente el de una partícula libre, las coordenadas ángulo-acción conservan el carácter ortogonal y cartesiano de las variables impulso y posición. O sea: de una cuadrícula en el plano x-p pasamos a la misma cuadrícula pero con otros nombres para las variables canónicas. En clase notamos que bastaba  ’redondear’ un poco el potencial para curvar las líneas coordenadas del nuevo sistema, pero no hicimos ningún cálculo explícito.

Lo que se muestra en los siguientes videos es la transición entre el sistema de coordenadas ángulo-acción para un potencial 1D que se altera paulatinamente desde V(x) = |x|, hasta V(x) igual al pozo infinito,  pasando por el potencial del oscilador armónico. El potencial es de tipo exponencial. La primera imagen ilustra todo el rango de exponentes considerados, entre 1 y 150.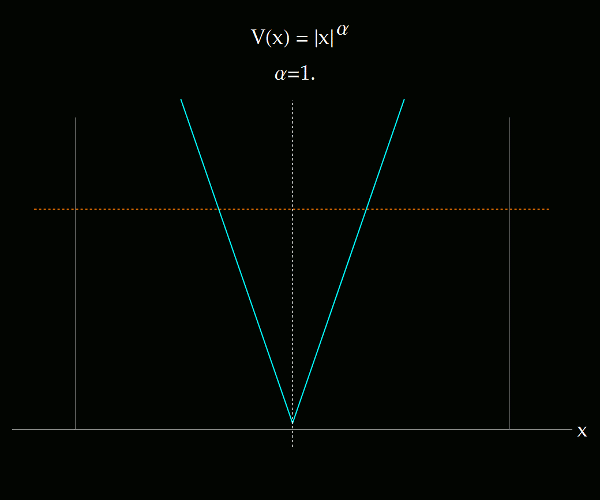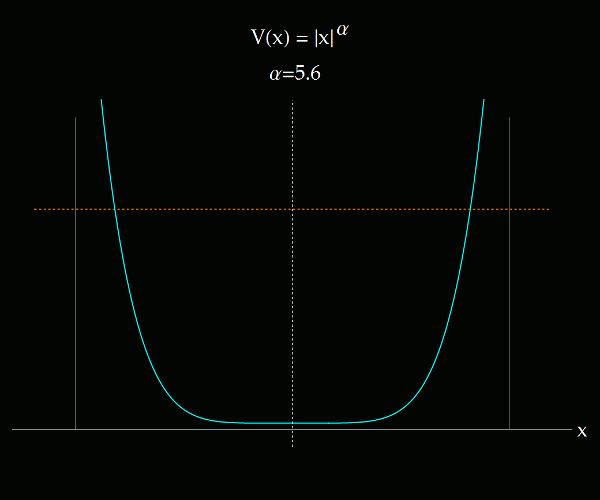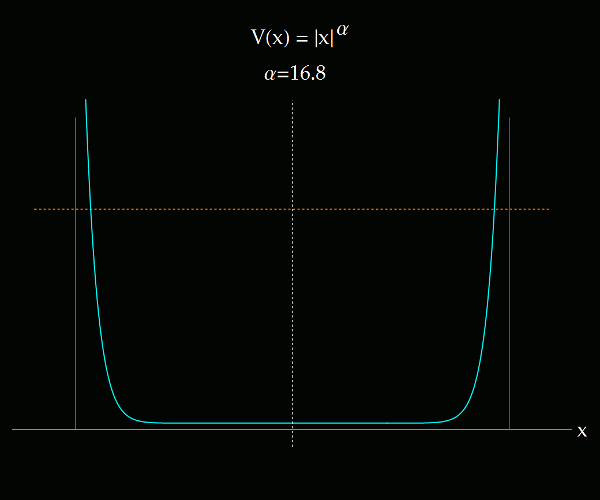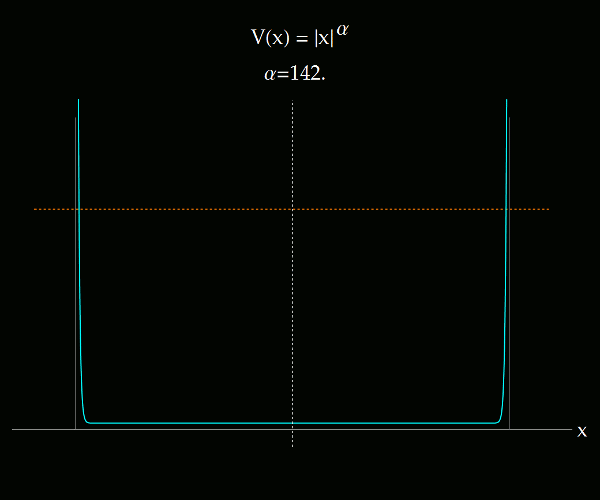

Para cada valor de α hay un sistema de coordenadas canónicas ángulo-acción que definen en el plano x-p sus propias curvas coordenadas. Las curvas coordenadas asociadas a la variable angular son típicamente radiales; las asociadas a la variable acción rodean al origen. Cuando el potencial tiende al pozo infinito, salvo para energías muy bajas (donde la partícula aún es sensible a la parte suave del potencial), las curvas coordenadas de las variables ángulo-acción tienden a la cuadrícula definida por las variables x-p. Vedlo en el siguiente video (con audio tenebroso). Recomiendo verlo en pantalla completa.

Las curvas coordenadas de la variable ángulo están numeradas como las horas del día.

En el segundo video se muestra una trayectoria en el espacio de fases para un valor intermedio del exponente α. La partícula cae desde el extremo x > 0 y se mueve sobre una de las curvas de energía constante. Sobre la trayectoria en el plano x-p están marcados 24 puntos que corresponden a 24 valores equiespaciados de la variable ángulo. La partícula tarda el mismo tiempo en moverse entre puntos consecutivos: esa es la propiedad que define a las variables de ángulo-acción, la isocronía. Esta vez con un audio luminoso, y también para ver en pantalla completa:

La descarga por ruptura dieléctrica en su rol social de pseudo justicia divina versus la palanca considerada como opresor de los inocentes y los desposeídos. (Seguir leyendo en Construcción social de los modelos físicos y su marco de influencia en el pensamiento pos kantiano...)

>Hola, Juan. Por favor, difundir a los posibles interesados.

Link en la imagen.

En la página Notas P1  se listan las notas del primer parcial.

Como hoy se notaron varias ausencias, y como queremos que tengan igualdad de oportunidades, aquí les repito,  para que puedan enterarse los que no vinieron, la información sobre una de las ayudas a las que pueden recurrir para el parcial:

José de Cupertino. Nació en 1602, en Cupertino, pueblito napolitano. Su familia era muy pobre. Porque no tardó en demostrar incapacidad para el estudio, sus padres lo sacaron de la escuela y lo colocaron de aprendiz de remendón; era tan desmañado que no logró aprender el oficio. A los 17 años entró como hermano lego en un convento franciscano; al poco tiempo lo despidieron, por inservible. Trató de ingresar en la orden de los Capuchinos, pero lo rechazaron. En 1621, por la recomendación de un tío suyo, lo admitieron en Santa María de Grosella, como oblato. Allá los padres superiores comprendieron pronto que, en su caso, la santidad se escondía bajo la rudeza y lo consideraron digno del sacerdocio.

El estudio fue para él un verdadero suplicio, porque sus facultades mentales eran escasas; sin embargo, pasó los exámenes milagrosamente y fue ordenado el 18 de marzo de 1628. Se retiró a orar. Durante los arrobamientos permanecía en suspenso en el aire, en suave levitación; por esto y por los milagros que le atribuyeron, intervino el Santo Oficio. Fue largamente examinado y se llegó a la conclusión de que no había “nada censurable en fray José”. Murió, como lo había predicho, el 18 de septiembre de 1663. Clemente XIII lo canonizó. Es patrono de los estudiantes y también, por ser llamado el Santo Volador, de los aviadores.

(En Descanso de Caminantes, de Adolfo Bioy Casares.)

Les acercamos un modelo de examen en este link para que vayan resolviendo, lo discutiremos el jueves en la clase práctica!