Buenas.
El lunes, luego de intentar resolver el misterio de las pequeñas oscilaciones del oscilador isótropo en torno a las órbitas circulares, empezaremos con la guía 4 que ya está subida.
Buen fin de semana.

Buenas.
El lunes, luego de intentar resolver el misterio de las pequeñas oscilaciones del oscilador isótropo en torno a las órbitas circulares, empezaremos con la guía 4 que ya está subida.
Buen fin de semana.
Es Catherine.
El scattering (dispersión) de partículas es un caso particular de fuerzas centrales, donde en vez de calcular de manera determinista la órbita de una partícula, tenemos un montón de ellas (flujo incidente) de las cuales no conocemos todas sus condiciones iniciales. Lo interesante del tema es que nos saca un poco del plano abstracto; en el labo no podemos controlar todos los parámetros y hay que inventarse observables que se relacionan a las condiciones que sí controlamos; uno de ellos es la sección eficaz.
Históricamente el tema es relevante debido a la importancia de un experimento en particular; el famoso scattering de Rutherford, un experimento hecho por Geiger y Mardsen allá por 1909, que llevó al descubrimiento del núcleo atómico propuesto por Rutherford en 1911. El otro modelo propuesto hasta el momento, el modelo de ‘budín de pasas’ (yo prefiero arroz con leche) de Thomson, donde los electrones estaban distribuidos sobre una masa de carga positiva, no lograba explicar los resultados.
En el modelo de Thomson, la conservación del momento y la energía en un choque elástico dictan que el ángulo debe ser inferior a 90º, si el proyectil es más masivo que el objetivo. Sin embargo, Geiger y Marsden demostraron que 1 de cada 8000 partículas alfa, se dispersaba con un ángulo mayor a 90º en el experimento de dispersión de Rutherford.
Les dejo un applet de PhET para que jueguen un poco con ambos modelos: applet.
En otras noticias, en la última clase vimos elipses que preceden. Si alguien pestañeó mucho y no la vio, acá hay un gif que puede ayudar cuando alpha=4/3.
Agradecimientos: todo el contenido útil del post fue propuesto por Max. Yo solo propuse el chiste inicial y él no quiso quedar involucrado. En agradecimiento tal vez, y solo tal vez, en alguna futura clase sea usada su notación.
El problema de los dos cuerpos interactuando mediante un potencial central está bien entendido en la física. En la clase del lunes vamos a ver algunos problemas de este estilo, siendo estos los problemas 6 y 9 de la guía tres. Nuevamente, pueden intentar plantearlos antes de la clase para ponerse a prueba.
Sin embargo, el problema de los tres cuerpos no tiene resolución analítica! Ya deben haber escuchado sobre esto, pero ahora están en posición de decir algo más: bajo una aproximación que podemos discutir, el problema de los tres cuerpos puede resolverse y dar soluciones útiles. ¿Son útiles estas soluciones aproximadas? Pueden esperar hasta el lunes, o se lo pueden preguntar al telescopio espacial James Webb. Aunque si pueden hablar con instrumentos avísenme que hay varias cosas que quiero decirle al osciloscopio!
Nos vemos!!
P.d1: la canción del principio originalmente iba a ser “Té para tres”, pero dado que estamos en vísperas de la fiesta de la primavera ponemos un tema un poco diferente. Aprovecho el espacio para recordarles que esta fiesta es el martes 20 y nos ayudan un montón a quienes viajamos al congreso de Bariloche si asisten! Además se ayudan ustedes porque la van a pasar genial.
P.d2: el lunes hay llamado a paro, así que es muy probable que la clase sea pública, en el pasillo entre el pabellón 1 y el 0+inf, como la de la otra vez.
Buenas. Ayer alguien se olvidó una campera en el aula. La tiene Nico, el lunes la lleva.
Si nadie la reclama, será subastada y las ganancias serán donadas a alguna fundación protectora de pingüinos para reparar algo de todo el daño que ustedes les han hecho desde física 1.
Buen fin de semana.
Buenas.
Retoqué un poco el enunciado del problema 13 de la guía 2, para incluir algo de la discusión que surgió sobre el final de la clase pasada. Mañana retomamos esa discusión y, después, empezamos a ver algo de la guía de fuerzas centrales, que ya está subida.
Nos vemos.
Al hablar sobre el hombre araña algunas personas querrán fotos y otras pensarán en multiversos. Sin embargo, está claro (?) que la mayoría va a pensar en la mejor versión del héroe de Marvel: el Julián Álvarez de 2021.
En cualquier deporte la técnica juega un rol fundamental: esta se puede definir como la economía temporal del movimiento, y, por este motivo, disponer de una buena técnica representa una ventaja muy grande en cualquier disciplina que requiera resolver situaciones en tiempos y/o espacios reducidos. En particular, en el video, se puede ver como el jugador recibe un pelotazo largo con una pierna y le pega con la otra, haciendo todo muy rápido y de manera fluida.
Los sistemas físicos en la mecánica clásica también siguen un patrón similar. Al mejor estilo F1, la dinámica de un sistema clásico se describe mediante las ecuaciones de Newton. Luego, vimos que la descripción dinámica puede hacerse a través del lagrangiano, recuperando la misma dinámica que con Newton, pero con ciertas ventajas operacionales.
Para describir la dinámica del sistema con el lagrangiano se usan las ecuaciones de Euler-Lagrange. Estas ecuaciones pueden seguirse desde las de Newton, junto con el principio de los trabajos virtuales, y algunas hipótesis más, pero también se pueden obtener partiendo de un principio fundamental: el principio de mínima acción.
Este principio dice que la evolución dinámica de los grados de libertad de un sistema físico, desde un tiempo inicial hasta otro final, es aquella que hace extrema una cierta cantidad, llamada casualmente “acción”. La acción se define como la integral temporal del lagrangiano, integrando desde el tiempo inicial hasta el final.

En este caso, S es la acción, y L es el lagrangiano. Se puede ver que este sistema dispone de un único grado de libertad, representado por la coordenada generalizada “x”. Digamos algunas cosas técnicas:
- La acción es una funcional, es decir, es una función de funciones. Esto es así debido a que, para calcular la acción, es necesario escribir explícitamente la dependencia temporal de las coordenadas generalizadas. En el ejemplo, para poder hacer la integral necesitamos tener x(t) (y por derivación dx/dt) y reemplazar estos valores en el lagrangiano. De esta forma tenemos todo en función del tiempo y podemos hacer la integral. Entonces el valor de S depende de las funciones q(t), es decir, de la dinámica de las coordenadas generalizadas.
- Por lo dicho anteriormente, para calcular un valor de la acción necesitamos conocer la evolución temporal de todos los grados de libertad del sistema. Ustedes ya vieron que variando la acción, salvo en el punto inicial y final, se obtienen las ecuaciones de E-L. Es decir, al “pedirle” a los grados de libertad que evolucionen de forma tal que hagan que la acción sea extrema, las coordenadas generalizadas “prefieren” evolucionar según las ecuaciones de E-L.
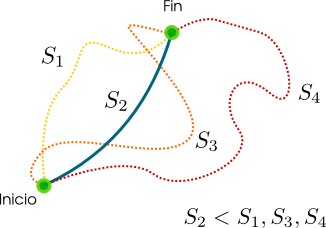
Este concepto no solo aparece en la mecánica clásica. De hecho, cualquier funcional S definida de forma similar será extrema cuando las funciones de las que dependa cumplan las ecuaciones de Euler Lagrange. De esta forma se puede calcular, por ejemplo, la curva que minimiza la distancia en cualquier geometría (seguramente en la guía de ejercicios les piden encontrar la curva que minimiza la distancia al desplazarse sobre un cilindro, por ejemplo).
Volviendo a la técnica deportiva, parece conceptualmente interesante discutir si la mejor forma de llevar a cabo un gesto técnico, tal como recibir la pelota, sea tal que minimice alguna funcional. Por ejemplo, en el próximo video se puede ver como con un movimiento muy simple, Matías Suárez simplifica la jugada de forma sublime. ¿Habrá hecho completa la guía 2 de mecánica clásica?
Viéndolo de esta forma, podríamos pensar que lxs jugadorxs de jerarquía son aquellxs que constantemente buscan minimizar esta funcional abstracta y desconocida, y que podemos aprender física en cualquier momento y en cualquier lugar!
P.d: en vísperas del superclásico, y sin la intención de mostrar favoritismo por alguno de los equipos, además de poner un video en el que aparece Belgrano, dejo también un lindo gol de boca. Para no quedar mal, je.
Vpython es una librería de Python que permite hacer gráficos 3D, se importa bajo el comando import vpython. Con una línea tan simple como sphere() ya tenemos una esfera! Casi que le saca la gracia.
Si instalar programas y Anaconda no es lo tuyo, existe una manera simple y online de usar Vpython sin instalar nada: Glowscript. Es como el Overleaf de Pyhton, solo te hacés una cuenta y listo, a tresderizar.
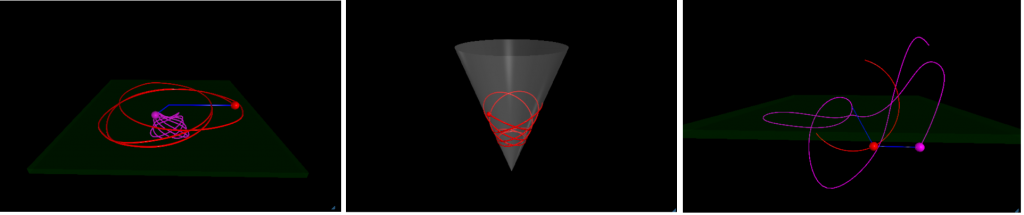 Acá pueden encontrar una simulación a algunos problemas de la guía 1: P5-Mesa , P8-Cono , P11-PenduloDoble .
Acá pueden encontrar una simulación a algunos problemas de la guía 1: P5-Mesa , P8-Cono , P11-PenduloDoble .
Algunas otras simulaciones (un poco al azar) las encuentran aquí: https://www.glowscript.org/#/user/maxx.coppola/folder/MyPrograms/ .
Las ecuaciones diferenciales se resolvieron usando el método de Euler de un paso, que es el más simple que existe para resolver numéricamente ecuaciones diferenciales.
Contenido confidencial, no seguir leyendo.
En otras noticias, pueden encontrar algunos pocos apuntes de la materia hechos durante la virtualidad acá .
Iremos subiendo más a medida que pasen las guías, la idea es que ustedes intenten hacerlos por su cuenta primero.
El Rastrojero nació tras un error. Por 1950, Argentina importó 2500 tractores Empire desde Estados Unidos, que debieron ser sacados de circulación porque, al estar preparados para el transporte de materiales militares y no para el trabajo agrícola, provocaron una gran cantidad de accidentes. Pero los tractores poseían increíbles motores y otras piezas útiles, era solo cuestión de ingeniárselas para reutilizarlos. Así nació en Córdoba el Rastrojero, un “mini-tractor’ nacional y popular, duradero y baratito, de los pocos autos producidos en el país. Aunque su fama definitiva la alcanzó cuando los 2500 motores se acabaron y se pasaron a diesel, abaratando enormemente los costos. Podías ahorrar $800.000 cada 100.000 Kms! Hablando en pesos ‘’de antes’’, claro. Otra cosa más que nos quitó la dictadura…
En 1641, el capitán holandés Willem van der Decken realizó un peligroso viaje a las Indias del Lejano Oriente, para comprar productos exóticos. A la vuelta quedó atrapado en una feroz tormenta. El agua acabó entrando en la embarcación, pero el capitán rehusó volver, desafiando la ira de Dios. Bien picante, se sometió a un pacto blasfemo con el Diablo para poder surcar siempre los mares sin importar los retos naturales que pusiera Dios en su travesía. Pero Dios, omnisciente, se entera de esto y en castigo lo condena a navegar eternamente sin rumbo y sin tocar tierra, ganándose el nombre de «Holandés errante».
A lo largo de la historia existen varios registros de barcos que dicen haber visto al holandés errante, u otros barcos fantasmas. Junto con los barcos también se han avistado miles de islas fantasmas como la Tierra de Crocker (norte de Canadá) y Sannikov (norte de Rusia), la isla Emerald (sur de Nueva Zelanda) que apareció por última vez en un Atlas de 1987, o la Isla Sandy (este de Australia) que se eliminó de Google Maps recién en 2012. Con un poco de suerte, ustedes podrían avistar algunos de estos fantasmas y subirlos a Tik Tok, volviéndose insta-famosos.
¿Cómo? ¿Que qué tienen que ver el holandés errante con un rastrojero? No, no es Helena Bonham Carter. Lo que tienen en común es el principio de mínima acción.
Mañana se los contamos.
Buenas.
Ya está subida la guía 2, sobre principios variacionales y el hermosísimo teorema de Noether.
El jueves arrancamos con esto en la práctica.
Abrazos.

“El hombre de negro huía a través del desierto y el pistolero iba en pos de él”
Así comienza la Torre Oscura, la obra maestra de Stephen King. Esta novela cuenta la historia de Rolando, el Pistolero, quien tiene como objetivo en la vida alcanzar la torre oscura. Para llegar a ella, el camino del protagonista comienza persiguiendo al hombre de negro: un hechicero misterioso y malvado, pero que será su guía si es que puede seguirle el paso.
Cabe destacar que en un momento de la historia, el hombre de negro reflexiona: “What did the universe ever do for me that I should mind its welfare?” Esta reflexión bien podrían hacerla los vectores posición con respecto a quienes necesitan perseguirlos: ustedes.
Nuestra torre oscura es el lagrangiano. El único objetivo en la vida de alguien que cursa meca debe ser alcanzarlo, y, aunque a veces puede parecer lejano o difícil, siempre podemos perseguir a nuestro hombre de negro.
¿Por qué el vector posición es nuestro hombre de negro? Piensen esto: si conocen los vectores posiciones de todas las partículas de un sistema con vínculos holónomos, expresados en términos de las coordenadas generalizadas (o sea, con los vínculos ya impuestos), entonces solamente haciendo derivadas y elevando al cuadrado tienen la energía cinética. Luego, en general, los potenciales dependen de posiciones y de estos mismos vectores las pueden leer!
Entonces, si trabajan lo suficiente como para escribir los vectores posición con los vínculos impuestos, lo que sigue es, valga la redundancia, súper mecánico! Obviamente conocer algunos trucos, y practicar mucho, puede ahorrar cuentas (y valioso tiempo en el parcial).
En la clase práctica del lunes vamos a resolver, además de otros, el ejercicio 14. Si tienen ganas intenten iniciar el camino a la torre por su propia cuenta y vemos hasta donde llegan!