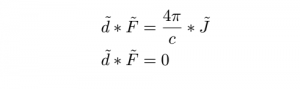Este post es un “refrito” de uno del año pasado publicado por Guillem Las 20 ecuaciones de Maxwell en el cual se destaca la belleza y la simpleza de las ecuaciones de Maxwell escritas en términos de formas diferenciales.
En el trabajo original de Maxwell las ecuaciones diferenciales para el electromagnetismo eran 20 en total
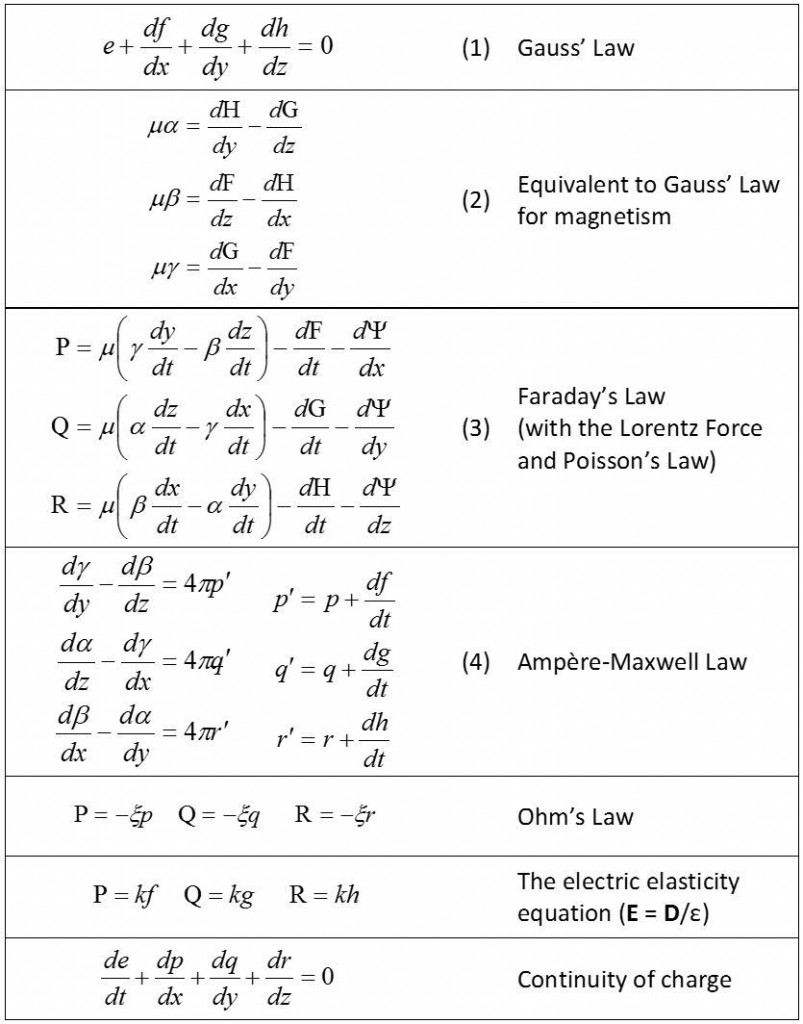
Posteriormente, Heaviside las agrupó en la notación habitual de cálculo vectorial (como en F3)

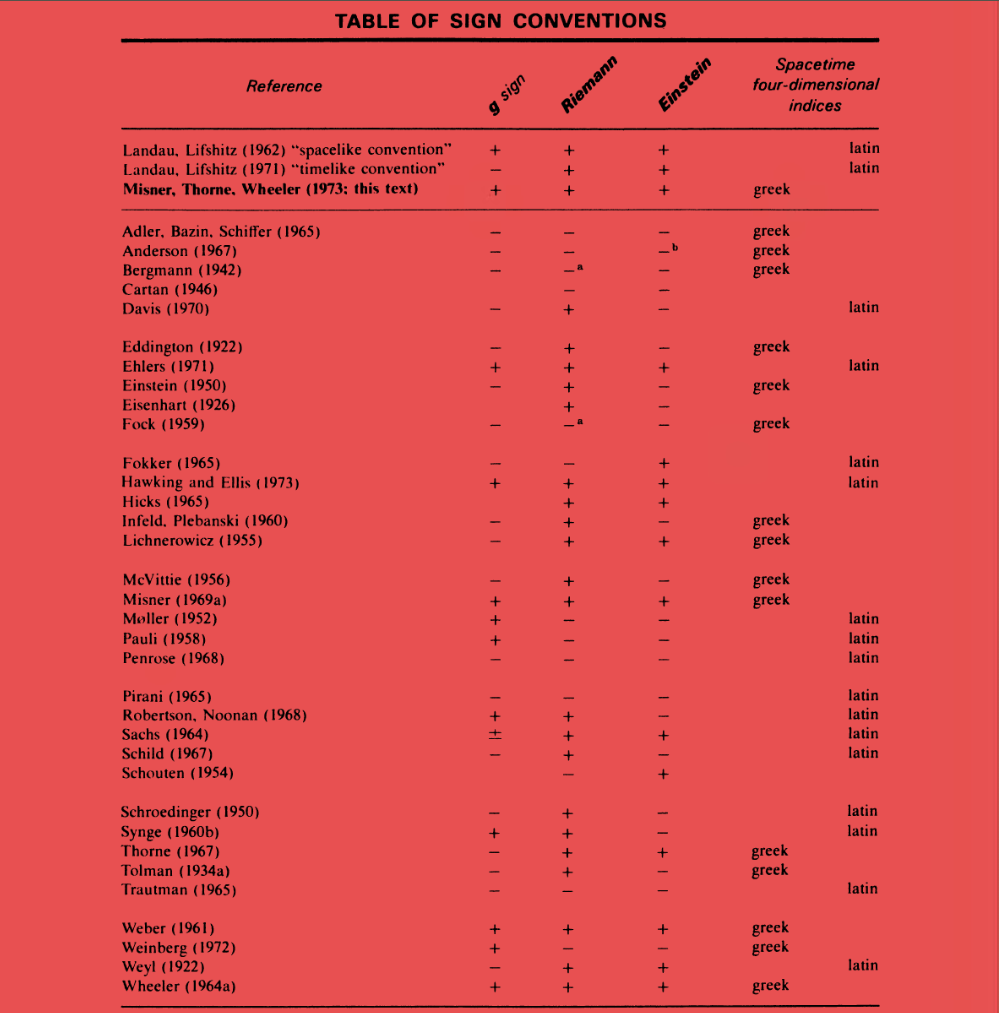
Como habrán visto el Física Teórica 1 y en parte del ejercicio 11 de la primer guía es posible escribirlas de una forma covariante

La mayor simplificación posible se logra usando cálculo exterior sintetizando todo en dos simples ecuaciones
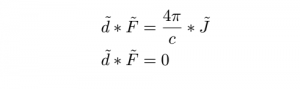
Citando a Guillem: “Más no se puede simplificar!”