“Hey ho, let’s go
Shoot ‘em in the back now
What they want, I don’t know
They’re all revved up and ready to go“

Tommy Ramone y Dee Dee Ramone, Blitzkrieg Bop (1976).

Al igual que Spiderman, ustedes eligieron estudiar física. Lo que ustedes quieren para su futuro, yo no lo se. Pero espero que estén acelerados y listos para conseguirlo. ¿Saben qué van a hacer después de graduarse? Usualmente, al terminar las clases teóricas de Física Teórica 1, yo dedico una clase para hablar específicamente sobre este tema. Hoy lo haremos en el aula, pero aprovecho este medio para complementar lo que les voy a contar volcando más información y reflexiones acá, esperando que les resulte útil para pensar qué cosas quieren y para que estén listos para conseguirlas.

Una de las características menos positivas de nuestra facultad es que pocas veces se discute en el aula cómo funciona la vida profesional de un graduado, qué opciones existen, y qué cosas va a esperar el mundo laboral de ustedes cuando se reciban. Los estudiantes tampoco preguntan mucho, tal vez pensando que preocuparse por esos temas mundanos los alejará de la imagen idealizada que construyeron de la ciencia. Pero independientemente de lo que ustedes quieran hacer, desde algo muy aplicado en la industria, hasta ciencia básica en una institución puramente académica, o investigación en una institución con una misión específica como la CNEA, el INTI o la CONAE, difícilmente lo consigan si no lo planean. El mundo profesional tiene reglas, y es bueno informarse y preparase para el momento en que se reciban, y para que puedan hacer lo que quieran en forma realista pero sin perder sus ideales.

El primer paso en su futuro más inmediato involucrará buscar temas de Laboratorio 6 y 7, y para la tesis de Licenciatura. Déjenme comenzar con tres consejos: Primero, más allá de los temas que los hayan motivado a estudiar física cuando empezaron la carrera, permítanse abrir sus horizontes y hablen con profesores e investigadores que trabajen en temas muy variados. Si después de cursar buena parte de la carrera no conseguimos generar en ustedes un interés amplio por la física en general, hemos fallado terriblemente como profesores. Hay cosas divertidas e interesantes en cada rincón de la física, y están en un momento ideal para descubrirlas y disfrutarlas.

Mi segundo consejo es que a la hora de buscar temas para el trabajo de Laboratorio y de Licenciatura, miren no solo el interés que el tema les despierta, sino también la calidad humana y docente del grupo en el que llevarían adelante el plan de trabajo. El principal objetivo que tiene el Departamento de Física y nuestra facultad no es que ustedes hagan algo revolucionario en esta etapa. Nuestro objetivo es que ustedes aprendan. Busquen grupos que se preocupen por enseñarles cosas, que los contengan y apoyen, y que se interesen por su futuro. Todo lo que aprendan en esta etapa, y lo que los profesores e investigadores compartan generosamente con ustedes, les va a servir mucho más en las próximas etapas que un título rimbombante en su plan de tesis.

Mi tercer consejo es que armen un calendario para sus próximos años. Si quieren hacer un doctorado, sepan que las becas no empiezan cuando ustedes quieren. Hay fechas estrictas para aplicar (y ustedes deben cumplir ciertas condiciones), y también para el inicio de las becas. No tiene sentido que se apresuren a recibir si las becas empiezan seis meses después que ustedes se recibieron, o que decidan tomarse seis meses de descanso para descubrir que por eso se recibirán dos meses más tarde que el inicio de las becas y deberán esperar un año más para comenzar el doctorado. Planifiquen para llegar cómodamente a las etapas importantes ordenando las materias que van a cursar y rendir en un calendario, aunque solo sea un calendario mental. No dejen muchos exámenes finales pendientes para cuando estén por terminar la carrera. Y sí, los planes pueden cambiar y pueden tener que recursar una materia. O una pandemia puede retrasar sus planes de dar exámenes finales. Cambiar planes es parte de la vida. Pero siempre es mejor tener un plan.

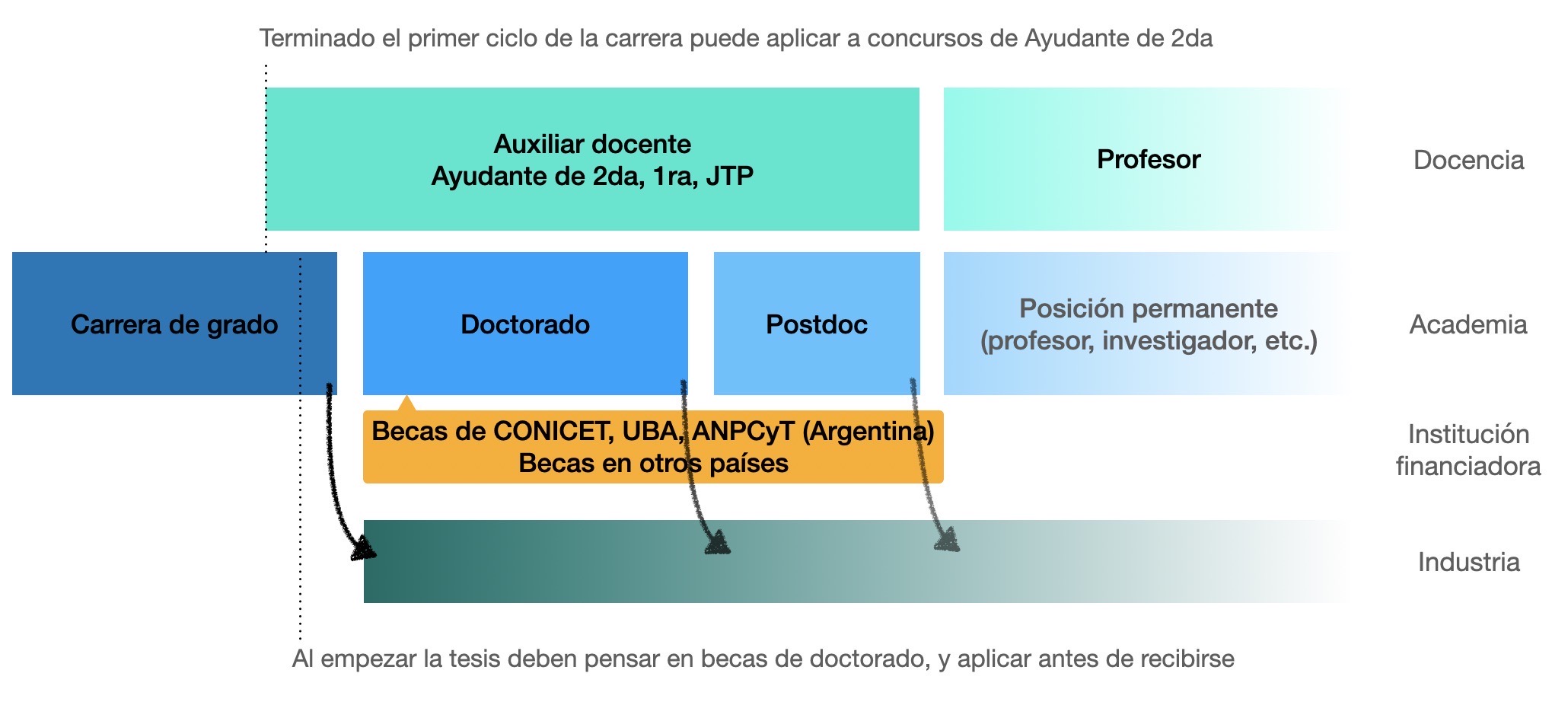
Para armar un buen calendario, tienen que conocer mínimamente las etapas que siguen en la vida profesional de un físico después de graduarse. Y aunque las variantes son tan grandes como el número de físicos en el mundo, y los esquemas deben ser tomados como lo que son, el siguiente esquema muy general les puede resultar útil:

Hacer docencia, al menos al nivel de docente auxiliar, es independiente de si deciden ir a la academia, a la industria o trabajar en otros ámbitos. La facultad y El Departamento de Física concursan todos los años más de 50 cargos rentados para Ayudantes de Segunda (solo en el área de física), pensados para que los estudiantes pueda tener esta oportunidad. Y en esta etapa de sus carreras, yo les aconsejo fuertemente que lo intenten. Los va a ayudar a seguir aprendiendo (¡como dijo Richard Feynman, cuando quieran aprender algo nuevo, intenten enseñarlo!). También los va a ayudar a ordenar sus ideas y aprender cómo contarlas en público. Y al aplicar a becas o buscar trabajo, la experiencia docente a nivel universitario tiene valor.

Luego de recibirse, pueden ir a la industria o hacer un doctorado. Y luego del doctorado pueden buscar una posición laboral en la academia, o un trabajo en una institución del sistema de ciencia y tecnología con una misión específica. O pueden hacer un doctorado y luego ir a la industria. Hay industrias en el país que buscan físicos, y el número de puestos de trabajo para los graduados y doctores en física aumentó notablemente desde que muchas empresas que hacen análisis de datos o modelado bursátil y financiero toman físicos para problemas que son interesantes y novedosos. Si les gustan esos temas, sacudan cualquier prejuicio que la academia pueda haber generado en ustedes. Y sepan que la empresa que los tome lo hará porque su forma de pensar y resolver problemas es útil, no por saber programar en Python o en C (eso se aprende rápidamente, y ninguna empresa busca un graduado o doctor en física por ese motivo). No voy a dedicar mucho espacio a este tema por cuestiones de tiempo, pero si les interesa les aconsejo que hablen con alguno de los muchos graduados de la carrera que se desempeñan en estas áreas. Los que quieran saber más sobre qué cosas puede hacer un graduado de física en la industria pueden también mirar estos artículos:

• “La industria de la física”, entrevista a Carlos Vignolo (BASF) por NEXciencia (es particularmente interesante su opinión sobre el valor de un doctorado para trabajar en la industria).
• Una entrevista a Sofía del Pozo, graduada del DF, en La Nación. Sofía trabajó como física en un banco, y forma parte de muchos graduados del DF que trabajaron o trabajan en industrias del conocimiento en el país y el extranjero. Tienen más ejemplos sobre graduados en la industria en esta nota.
• La página de DF Innova, y miren especialmente las ofertas laborales.

Ya sea porque quieren trabajar en ambientes más académicos (donde, en física, un doctorado es una condición necesaria para poder investigar en forma independiente), o porque quieren trabajar en una empresa pero siguiendo los consejos de Vignolo prefieren hacer un doctorado primero, en unos años se encontrarán frente a la pregunta de cómo hacer un doctorado. Si quieren hacer un doctorado en el país, tengan en cuenta que un doctorado es una actividad de dedicación completa, y salvo casos excepcionales requiere una beca. Hay muy buenos grupos de investigación, y el doctorado de la UBA es prestigioso. Para poder hacerlo hay tres mecanismos de financiación que son los más usuales:

• Las becas de doctorado del CONICET.
• Las becas de la UBA.
• Becas financiadas dentro de proyectos de la ANPCyT.

Les aconsejo que sigan los links y conozcan las instituciones que pueden llegar a financiar su doctorado. Y se informen sobre las reglas de, al menos, los llamados del CONICET y la UBA (en el caso de ANPCyT, como las becas están ligadas a proyectos de investigación, quien sea su director o directora se encargará de esos detalles). Algunas becas tienen límite de edad para poder aplicar. Otras tienen otro tipo de condiciones. Tomen por ejemplo el llamado a becas del CONICET. Usualmente se realiza en los meses de julio o agosto, para comenzar el doctorado el 1 de abril del año siguiente. Y al momento de aplicar, el CONICET les pide que no deban más de 6 finales incluyendo la Tesis de Licenciatura (los últimos años fueron excepcionales por la situación generada por COVID-19).

Discutir las etapas que siguen en la vida profesional de un físico luego del doctorado alargarían innecesariamente esta carta de cierre de la materia. Déjenme entonces cerrar con un último consejo. No tengan miedo a cambiar de tema a lo largo de su carrera profesional, y a trabajar con diferentes personas y grupos, en diferentes lugares e instituciones (obviamente, cambiando al terminar las diferentes etapas de formación, y no tratando de hacer varias cosas al mismo tiempo a lo largo de una única etapa como en la Tesis de Licenciatura). Es bueno, y además de brindar una visión más amplia de la física, ayuda a conocer qué prácticas científicas queremos aprender para nuestro futuro y cuáles no. Y elijan trabajar con gente con la que se sientan a gusto. Toda la carrera científica es una carrera de aprendizaje, pero las primeras etapas son muy especiales y marcan lo que más adelante le podemos enseñar a quienes trabajen con nosotros.

Espero que hayan disfrutado esta materia tanto como yo disfruté enseñarla. Y que las clases les hayan resultado interesantes y formativas. Si esta es la última Física Teórica que cursan, es probable que no nos volvamos a encontrar en un aula (al menos mientras sean estudiantes de grado). Les agradezco la paciencia en este cuatrimestre y espero que les haya gustado el curso. Y a todo el resto, espero verlos nuevamente en algún aula. Mucha suerte en el parcial, y nos reencontraremos en el examen final.

Con este posteo comenzamos un ciclo sobre las aplicaciones del electromagnetismo (y la ciencia en general) en la guerra. Y qué mejor que comenzar con la escena del coronel Hans Landa hablando italiano en Inglourious basterds, película de 2009 dirigida por Quentin Tarantino, y una de las mejores películas bélicas de los últimos tiempos (disponible en Netflix). Los que tengan sed de películas bélicas también pueden mirar El gran escape (1963), un clásico con Steve McQueen que fue recientemente homenajeado en otra película (no bélica) de Tarantino, y Darkest hour (2017), una película que le dio el Oscar a Gary Oldman por su impresionante interpretación de Winston Churchill (también disponible en Netflix).

Por primera vez en la historia de la humanidad, la segunda guerra mundial encontró a los países enfrentados con una comprensión amplia del electromagnetismo y sus aplicaciones. Y diversas invenciones jugaron un rol preponderante en el desarrollo de la guerra. Winston Churchill, primer ministro del Reino Unido durante la guerra, llamó al uso de la ciencia durante la guerra “la guerra de los magos“, en una serie de libros que le dieron el premio Nobel de literatura:

“Durante la lucha humana entre las Fuerzas Aéreas Británicas y Alemanas, entre piloto y piloto, entre baterías antiaéreas y aviones, entre bombardeos despiadados y la fortaleza del pueblo británico, otro conflicto se desarrollaba paso a paso, mes a mes. Se trataba de una guerra secreta, cuyas batallas se perdían o ganaban sin que el público lo supiera, y que aún ahora pueden apenas ser comprendidas, con dificultad, por las personas ajenas a los pequeños círculos involucrados. Nunca hombres mortales habían librado semejante guerra. Los términos en los que se podía hablar o registrar eran ininteligibles para la gente común. Sin embargo, si no hubiéramos llegado a dominar su profundo significado y utilizado sus misterios, incluso cuando apenas los vislumbrábamos, todos los esfuerzos, todas las destrezas de los aviadores, toda la valentía y los sacrificios del pueblo habrían sido en vano. A menos que la ciencia británica hubiera demostrado ser superior a la alemana, y a menos que sus extraños y siniestros recursos se hubieran aplicado eficazmente a la lucha por la supervivencia, bien podríamos haber sido derrotados, y al ser derrotados, destruidos.“

Winston Churchill, Their finest hour (1949)

Una de las invenciones que tuvieron un rol importante fue el radar. El radar tiene una relación directa con los experimentos de Heinrich Hertz para detectar ondas electromagnéticas que vimos antes del parcial. Un radar consiste en una antena que emite ondas electromagnéticas (originalmente, en la región del espectro de las ondas de radio). Si hay un obstáculo (como un avión o un barco), parte de la onda electromagnética se refleja, y la reflexión es detectada por la misma antena que emite la señal. De esta forma, el radar permite obtener información de la posición de diferentes objetos (y de la velocidad a la que se mueven si se mide el corrimiento de la señal reflejada por efecto Doppler).

Antes de la invención del radar los aviones se detectaban con una serie de personas en tierra que miraban el horizonte, y daban la señal de alarma al avistar naves enemigas. Obviamente, esto permitía prepararse para un bombardeo con muy poco tiempo. Y los aviones y los barcos no podían ser vistos en condiciones meteorológicas adversas (por ejemplo, en presencia de nubes bajas o si toda una región estaba cubierta por niebla). La invención del radar cambió esto, y cambió también las estrategias de ataque y defensa. Quien tuviera primero una red de radares instalada, tendría una ventaja sobre el enemigo.

Hacia 1939 el Reino Unido había construido una amplia red de radares, que fue seguida más tarde por la construcción de una red equivalente en Alemania. Pocos años después se comenzaron a montar radares en los mismos aviones, para permitir el bombardeo nocturno o con niebla. Ahí se reconoció la importancia de cambiar la longitud de onda de funcionamiento de los radares: la señal de radio tiene una longitud de onda entre 1 y 1000 metros, lo que genera una incerteza importante a la hora de posicionar los blancos. Usar microondas, con una longitud de onda mucho menor, mejora substancialmente la determinación de la posición (este cambio también resultó, en parte fortuitamente, en la invención del horno a microondas).

En esa época también se desarrollaron los primeros métodos para engañar a los radares, y los alemanes y británicos descubrieron independientemente que podían distraer al operador de un radar, generando falsos avistamientos de aviones, lanzando al aire muchas tiras pequeñas de papel metalizado con la longitud correcta.

El electromagnetismo también jugó roles importantes en el diseño de bombas y minas. El uso de “gatillos magnéticos” y otras variantes de gatillos permitió diseñar bombas que solo explotasen al acercarse suficientemente al casco de los barcos, o que explotasen luego de un intervalo de tiempo en lugar de hacerlo inmediatamente por contacto. Y obviamente, aunque tiene que ver con otras fuerzas, el proyecto científico más famoso de la segunda guerra mundial fue el Proyecto Manhattan en Estados Unidos, que tuvo como objetivo desarrollar una bomba nuclear. Aunque suelo recomendar la lectura en mis materias, para quienes no lo hayan leído antes, les dejo el link a las memorias del Proyecto Manhattan de un joven Richard Feynman (¡incluyen lecciones sobre como abrir cajas fuertes!):

• Los Alamos from below

Pará, pará, pará… En el último post explicamos alegremente que las nubes se cargan por las colisiones entre cristales de hielo y graupel, de la misma forma que el vidrio se carga al frotarse con lana, o nuestro pelo al frotarse contra un globo. Hasta Bart Simpson lo sabe. Y esto está muy bien, Tales de Mileto (el del famoso teorema de Tales) ya sabía que el ámbar se carga eléctricamente al ser frotado con otros materiales. Estas primeras observaciones realizadas en la antigua Grecia (o más precisamente, en lo que hoy es Turquía) luego dieron inicio al estudio de las cargas eléctricas y a la electrostática. Jorge Luis Borges menciona las contribuciones de Tales en uno de sus poemas:

“Fue, en las cosmogonías, el origen secreto
de la tierra que nutre, del fuego que devora,
de los dioses que rigen el poniente y la aurora.
(Así lo afirman Séneca y Tales de Mileto.)“

Jorge Luis Borges, Poema del cuarto elemento (1964).

Pero ¿por qué ciertos materiales se cargan al chocarlos o frotarlos? Es un fenómeno al que estamos acostumbrados, y uno de los primeros fenómenos asociados al electromagnetismo que conoció la humanidad. Lo damos por hecho, nos parece natural y hasta un efecto menor o fácil de entender (aunque no lo es). ¿Cuál es su origen? El efecto se llama “triboeléctrico“, y ponerle un nombre no alcanza para que lo comprendamos (de hecho, el nombre a mi me sugiere la existencia de alguna tribu eléctrica o algo parecido).

El  fenómeno no es para nada sencillo de comprender. La descripción somera es la siguiente: ciertos pares de materiales, cuando se frotan entre si (y de hecho, alcanza con que simplemente entren en contacto) se cargan eléctricamente, uno con un exceso de cargas positivas, el otro con un exceso de cargas negativas. No todos los pares de materiales se cargan de la misma forma cuando se los frota: algunos tienen tendencia a siempre perder cargas negativas (y resultar cargados positivamente, como el nylon), otros tienen tendencia a siempre ganar cargas negativas (como el polyester). Algunos pares de materiales se cargan más que otros al ser frotados. Estos materiales realmente ganan (o pierden) cargas, las cargas que obtienen luego de ser frotados no son cargas de polarización. Y si la diferencia de carga es lo suficientemente grande, cuando nuevamente entran en contacto recuperan el balance de carga por la ruptura dieléctrica del aire, produciendo una chispa.

El mecanismo físico por el que esto ocurre no está totalmente entendido. Pero involucra al efecto túnel cuántico. Cuando dos cuerpos entran en contacto, las nubes electrónicas de los átomos en la superficie de cada material se superponen. Cada átomo corresponde a un mínimo de potencial, separados por un máximo asociado a la repulsión electrostática entre los electrones de ambas nubes, como muestra esquemáticamente la siguiente figura:

Si un mínimo es más chico que el otro (por propiedades de cada uno de los dos materiales), los electrones pueden atravesar el máximo que los separa preferentemente en una dirección, ya sea por agitación térmica, por excitación por fotones incidentes, o por efecto túnel (es decir, el efecto por el cual la función de onda de un electrón con energía menor a la barrera de potencial puede propagarse a través de esa barrera, y el electrón puede ser encontrado con probabilidad no nula del otro lado de la barrera de potencial). Y al separar los materiales, esos electrones se quedan atrás, en el otro material. Cuántos electrones pasan depende de las propiedades de cada material (la amplitud de los potenciales, la humedad relativa en el ambiente, etc.).

Pero para que lo entienda mi tía, ¿vos estás diciendo que cada vez que nos peinamos ocurre efecto túnel cuántico entre los electrones en el peine y en nuestro pelo? ¿Vos estás diciendo que podemos hacer experimentos de efecto túnel en nuestras casas usando lana y un vidrio, y que hasta podemos medirlo? ¿Y vos estás diciendo que solo por entrar en contacto o frotarse, un material se queda con los electrones del otro? Sí, estoy diciendo todo eso. ¿Pero cuántos electrones le arranca el material por frotamiento? ¡No se, hagamos la cuenta! Ciertos pares de materiales pueden obtener por frotamiento una densidad de carga superficial de hasta σ = 150 μC/m². La carga de cada electrón es e = 1.6 x 10^-19 C. Luego, la cantidad de electrones arrancados puede ser

σ / e = 937.500.000.000.000 electrones por metro cuadrado.

Este parece ser un número enorme para intercambiar más tarde en una chispa:

Frank Miller, autor del cómic “Batman: The Dark Knight Returns“, dijo alguna vez que el personaje de Batman es como un gran diamante que no se puede romper. Lo pueden tirar contra el techo o contra el piso, lo pueden golpear con un martillo, pero no puede romperse. Cada interpretación, cada nueva encarnación de Batman, de alguna forma u otra funciona (pueden aprovechar y ver la trilogía del caballero de la noche de Nolan, que está completa en Netflix). Y Batman permea tanto en la cultura popular que la famosa frase usualmente atribuida a Robin en las traducciones al español ni siquiera le pertenece, aunque todos la asociamos a Batman y a Robin. El verdadero dueño de la frase “Rayos y centellas” es el ebrio capitán Haddock en el cómic Las aventuras de Tintín del belga Hergé.

¿Pero cómo se electrifica la atmósfera y se producen los rayos (y centellas)? El aire es un dieléctrico y no conduce la electricidad. Así que para que se produzca el rayo, el medio debe sufrir un proceso de ruptura dieléctrica y volverse conductor. Pero comencemos por el principio, viendo cómo se electrifica la atmósfera. Este es un ejemplo interesante de una aplicación de la teoría electromagnética en medios dieléctricos, y cuyos detalles solo han sido bien comprendidos en los últimos años. También, muestra que un dieléctrico solo funciona como aislante hasta un potencial de ruptura, y por encima de esa diferencia máxima de potencial los portadores de carga se liberan y el material se vuelve conductor. Quienes quieran ver otro ejemplo muy pintoresco (pero peligroso) asociado a la ruptura dieléctrica, también pueden leer sobre figuras de Lichtenberg (un fenómeno que además tiene características fractales).

La electrificación de una nube comienza de la misma forma que acumulamos carga electrostática cuando frotamos materiales dieléctricos (como un peine contra nuestro pelo): los electrones pasan de un material a otro, y se genera un exceso de carga en uno y un defecto en el otro. En las nubes ocurre lo mismo cuando cristales de hielo chocan y rozan contra el graupel (pequeños granos de hielo o granizo muy chico). Esto ocurre constantemente por la turbulencia dentro de la nube, que arrastra las partículas y las hace chocar unas contra otras. Las partículas más livianas y cuya superficie está creciendo más rápido por condensación (los cristales de hielo) se cargan positivamente luego de cada una de estas colisiones, mientras que el graupel gana electrones y se carga negativamente. La gravedad hace el resto del trabajo: las partículas livianas (positivas) tienden a acumularse más arriba, y las más pesadas (negativas) más abajo, generando un gradiente en la densidad de carga electrostática. A su vez, las cargas negativas en la base de la nube inducen una carga opuesta en la superficie de la tierra. Todo este proceso se ha conseguido observar y medir, en las últimas décadas, en experimentos bajo condiciones controladas en el laboratorio.

Luego que las cargas están separadas, el gradiente en la densidad de carga eléctrica (en altura, o en la dirección z) genera una diferencia de potencial y un campo eléctrico, ya que

Pero este campo eléctrico no es lo suficientemente intenso como para generar la ruptura dieléctrica del aire. Los materiales dieléctricos solo se “rompen” y se vuelven conductores cuando se alcanza el potencial de ruptura, que para el aire corresponde a un campo eléctrico de » 3 x 10⁶ V/m. Así, la ruptura dieléctrica en lugar de ocurrir en simultáneo a lo largo de toda la columna de aire que conecta la tierra con la nube, se inicia localmente en algún punto donde el gradiente de carga y el campo eléctrico es muy intenso. Esa ruptura a su vez genera nuevos gradientes de carga y de potencial entre los extremos de la region que sufrió la ruptura con el resto de la nube, y el “canal” de conducción que se forma se comienza a propagar en ambas direcciónes, hacia arriba y hacia abajo, generando el rayo.

Los que quieran una descripción más detallada desde el electromagnetismo del proceso de formación de un rayo pueden leer las primeras dos secciones del siguiente paper. Noten que el trabajo es de 2013, y todavía quedan muchas preguntas por responder:

• Theory and observations of controls on lightning flash size spectra (paper).

“Sun is shinin’ in the sky
There ain’t a cloud in sight
It’s stopped rainin’ everybody’s in the play
And don’t you know
It’s a beautiful new day, hey hey.“

Electric Light Orchestra, Mr. Blue Sky (1977),
también usada en la apertura de Guardianes de la Galaxia Vol. 2.

Pronto llega la primavera y el cielo cambiará de a poco la tonalidad de su color azul, por un efecto electromagnético que veremos al final del curso. Pero antes de explicar efectos tan complicados, el electromagnetismo tuvo su primer triunfo al asociar, en parte, los experimentos con cables y baterías de Faraday y de Ampère con lo que ven nuestros ojos: la luz y los colores.

Uno de los primeros logros de la teoría electromagnética de Maxwell fue identificar correctamente a la luz como radiación electromagnética. En uno de sus primeros papers sobre la teoría electromagnética, al reconocer que sus ecuaciones tenían soluciones en forma de ondas que se propagan a la velocidad de la luz, Maxwell hipotetizó que tal vez la luz fuera, simplemente, radiación electromagnética (aunque Faraday ya había jugado con esta idea, al notar en sus experimentos que con un campo magnético podía modificar la polarización de la luz). La diferencia entre las ondas de radio (que se descubrirían al poco tiempo) y la luz, es simplemente la región del espectro electromagnético que las diferentes ondas ocupan.

El espectro electromagnético visible es el que pueden ver nuestros ojos, y asociamos un color a cada longitud de onda:

Pero, ¿qué es el color azul? ¿Es simplemente una onda electromagnética con una longitud de onda cercana a los 460 nm? ¿Qué es el color rojo? ¿Y qué es el color rosa de aquella cosa que llamamos rosa?

“Si (como afirma el griego en el Cratilo)
el nombre es arquetipo de la cosa
en las letras de ‘rosa’ está la rosa
y todo el Nilo en la palabra ‘Nilo’.“

Jorge Luis Borges, El gólem (1958)

Estas preguntas no son retóricas, ni filosóficas, ni propias de Umberto Eco. Porque aunque como mencioné previamente el color azul del cielo se debe al electromagnetismo, la percepción del color azul no se limita simplemente a que nuestros ojos detecten una onda electromagnética en los 460 nm. Al menos en este caso, en las letras de la palabra ‘azul’ no está el azul. La percepción de los colores es increíblemente complicada e involucra al electromagnetismo, a la fisiología del ojo, y a las neurociencias.

Comencemos por algo sencillo. Nuestros ojos tienen dos tipos de células diferentes que son sensibles a la radiación electromagnética en el espectro visible: los bastones y los conos. La longitud de onda dominante en la luz determina el matiz (“hue“) que percibimos. Pero el matiz  (o la longitud de onda) no alcanza para determinar unívocamente el color que vemos.

Los bastones y los conos no tienen una sensitividad uniforme en todo el espectro. Los bastones son más sensibles a la luz y funcionan aún en ambientes con iluminación baja, pero tienen poca sensibilidad a las diferentes longitudes de onda. Por otro lado los conos son menos sensibles a la luz, pero tienen un mayor rango de sensibilidad a las diferentes longitudes de onda. Ellos son los responsables de que veamos en colores. Hay tres tipos de conos (básicamente, tres detectores que miden ondas en diferentes regiones del espectro). Dos tipos de estos conos tienen mayor sensibilidad entres los 520 y los 590 nm. Observen la imagen previa del espectro electromagnético: probablemente el color verde les parezca más intenso. Esto tiene que ver con la diferente sensibilidad de los conos a las diferentes longitudes de onda. La diferente sensibilidad a la luz de los conos y los bastones también hace que nuestra percepción de los colores cambie de acuerdo a la iluminación, o entre el mediodía y el atardecer. Un matiz rojo (es decir, con longitud de onda dominante de 620 nm) puede parecernos marrón de acuerdo a la iluminación. El ángulo en el que incide la luz sobre un material, y el espectro emitido por la fuente, también afecta nuestra percepción del color. Así, el color que percibimos depende no solo del matiz, sino también de la iluminación (y del brillo de la superficie entre otros detalles). Dado un espectro electromagnético en el rango visible, reconstruir un “color” a partir del mismo no es tarea fácil, y requiere tener en cuenta todas estas variables.

Como si esto no fuera suficiente, nuestro cerebro debe procesar la información proveniente de los bastones y los conos. Aunque el procesamiento de la información ocurre mayormente en la corteza visual, hoy se sabe que la información pasa antes por otras regiones cercanas del cerebro. Y la percepción de los colores se vuelve subjetiva, variando de un sujeto a otro. Recuerden todo esto cuando estén tentados en pensar que los colores que percibimos están simplemente definidos por la longitud de onda electromagnética dominante. Y los que tengan interés en temas más amplios de física y conciencia pueden mirar la página del grupo de neurociencias dirigido por Enzo Tagliazucchi (@Etagliazucchi) en el Departamento de Física.

En un momento de Interstellar, la película co-escrita y dirigida por Christopher Nolan, Joseph Cooper se encuentra viviendo en el interior de una nave espacial con forma de cilindro. El cilindro gira sobre su eje principal, y los habitantes de la nave sienten una aceleración centrífuga que sostiene sus pies en la tierra. El concepto original fue creado por un físico, Gerard O’Neill, y está relacionado con otras ideas sobre como viajar o sostener colonias interplanetarias, como la esfera de Dyson. Los que quieran conocer mas detalles sobre esta idea, y sobre cómo se usa en algunos clasicos de la ciencia ficción como “Mundo anillo” de Larry Niven, pueden mirar una charla de divulgación que di hace unos años.

Si alguna vez abrieron un televisor, una computadora, u otro artefacto eléctrico o electrónico, habrán notado que está lleno de cilindros pequeños y grandes, con dos patas:

Estos son capacitores cilíndricos. En el otro extremo, suelen tener una tapa metálica con una cruz. Cuando el capacitor falla, la tapa se hincha, o hasta puede abrirse y material dieléctrico salir por ese extremo. Así que ya saben, si tienen algo que se rompió en sus casas y al abrirlo encuentran capacitores como el de la foto, lo primero que pueden hacer es encargar repuestos y reemplazarlos con una soldadora:

¿Pero por qué se usan capacitores cilíndricos? Una razón tiene que ver con las herramientas que vemos en la materia. La existencia de soluciones formales para el problema electrostático en coordenadas cilíndricas permite diseñar este tipo de capacitores y calcular los potenciales y campos con mucho detalle. Pero además, los capacitores cilíndricos pueden tener más superficie (en el mismo volumen) que un capacitor plano, y por lo tanto pueden almacenar más carga. La mayoría de los capacitores comerciales no están formados simplemente por dos placas conductoras concéntricas separadas por vacío. Las dos placas conductoras, separadas por un dieléctrico (para aumentar la carga que el capacitor puede almacenar), se enrollan varias veces sobre si mismas para formar el cilindro. Así, las razones para usar capacitores cilíndricos son prácticas, y no tienen que ver con las películas de Nolan (aunque más adelante haré algunas recomendaciones al respecto). Y además de todo esto, los capacitores no son siempre cilíndricos, existen otros tipos de capacitores según el problema.

El método de separación de variables, los armónicos esféricos y las expansiones multipolares tienen aplicaciones en física que van mucho más allá de la electroestática y la magnetoestática. Y los armónicos esféricos no aparecen solo en estos problemas o en la solución del átomo de hidrógeno. Como forman una base completa, se usan para representar formas y deformaciones de la simetría esférica en forma unívoca en muchos problemas (aún si los problemas son no-lineales).

Por ejemplo, el campo magnético de la Tierra es mayormente dipolar. Pero el campo magnético tiene anomalías, regiones en la superficie de la Tierra en las que el campo magnético es menos intenso que la intensidad que correspondería al dipolo. Una de ellas es la anomalía del Atlántico sur:

Los armónicos esféricos se usan para caracterizar esta anomalía (y también la “forma” de los campos magnéticos de otros planetas). Los que quieran leer más sobre esto, pueden ver este paper sobre la anomalía del Atlántico Sur.

La anisotropía en la radiación cósmica de fondo (radiación electromagnética de cuerpo negro que fue emitida en el momento en que se formaron los primeros átomos en el universo, y que llega a nosotros proveniente de todas las direcciones) también se mide usando armónicos esféricos. La radiación cósmica de fondo es aproximadamente isótropa. Pero si se resta el valor medio a la radiación, la proyección de las fluctuaciones en la potencia de la radiación que nos llega de diferentes regiones del firmamento se ve así:

Lo que muestra esta imagen son las variaciones alrededor de la temperatura media asociada a la radiación de cuerpo negro que recibimos (el valor medio de la temperatura es de 2.725 grados Kelvin). Las regiones azules y rojas están, respectivamente, 0.0002 grados Kelvin a mayor o a menor temperatura que la media. ¿Cómo podemos caracterizar estas fluctuaciones y extraer información cuantitativa sobre su anisotropía? Proyectando sus amplitudes en la base de armónicos esféricos. La figura a continuación muestra el espectro de la radiación cósmica de fondo en términos del momento multipolar l. Es decir, la amplitud de cada modo cuando la radiación cósmica de fondo se proyecta en la base de armónicos esféricos Y_lm como muestra este gráfico tomado de Wikipedia:

¿Cómo leemos este gráfico? Si tuvieramos toda la amplitud de la señal de la radiación cósmica de fondo en el armónico esférico Y₀₀, entonces la radiación cósmica de fondo sería perfectamente isótropa, pues el armónico esférico con l = m = 0 tiene la misma amplitud en todas las direcciones. De hecho, la mayoría de la potencia en la radiación cósmica de fondo está en ese armónico esférico, así que para mirar la anisotropía ese modo se remueve. Por otro lado, tener picos en el resto de la señal en armónicos esféricos con l » 200, 550, y 800, nos dice que tenemos variaciones con aproximadamente ese número de ceros en la coordenada q (y probablemente también en f), o equivalentemente, que la radiación cósmica de fondo fluctúa con mayor amplitud con períodos que corresponden a ángulos subtendidos de » 1, 0.4 y 0.2 grados. Claramente la señal no se limita solo a esos armónicos esféricos y tiene contribuciones de otros modos. Pero podemos imaginar cómo la superposición de estos modos reconstruyen la señal mirando la siguiente figura, que muestra el armónico esférico con l = m = 1, el armónico esférico con l = 10 y m = 5, y una superposición de solo 5 armómicos esféricos con valores de l entre 1 y 40 con fases al azar:

Los picos en el espectro (el valor de l en el que ocurren, y su amplitud y forma) tienen información física. Como la radiación cósmica de fondo se generó en una etapa temprana del universo, se pueden usar esta información para estimar parámetros importantes en cosmología, como la curvatura media de nuestro universo, o la densidad media de masa y energía en el universo. De esta forma sabemos que el universo es, en buena medida, plano.

Los armónicos esféricos también se usan para estudiar la emisión de ondas gravitatorias por la colisión de dos agujeros negros. Las fuentes (los dos agujeros negros) ocupan una región acotada del espacio, y emiten ondas que se pueden describir con una expansión multipolar en términos de los armónicos esféricos. Los que quieran tener una idea de cómo se hace esto pueden ver este documento técnico.

Para los que tengan más interés en estos últimos temas, en el Departamento de Física Gastón Giribet (@GastonGiribet), y el Grupo de Física Teórica de Altas Energías en el que están Emilio Rubín de Celis (@EmiRubindeCelis) y Matías Leoni (nuestros Jefes de Trabajos Prácticos), trabajan en problemas relacionados con los agujeros negros (entre otros grupos trabajando en temas afines en el Departamento).

Por suerte Sting no sabe expresar formas y deformaciones en términos de armónicos esféricos, y en lugar de hacer proyecciones en los elementos de esta base, escribe canciones para describir la forma de su corazón.

En 2010, Scott Pilgrim fue adaptado al cine (la película está disponible en Netflix). Si bien fue un fracaso en taquilla, y el personaje de Scott en la película por momentos puede ser irritante, la película captura muy bien la estética del cómic original y más tarde se volvió una película de culto. Superman, Capitán América y Capitana Marvel aparecen en la película (¡no en esos roles!). Y el director, Edgar Wright, dirigió varias películas interesantes, entre las que les recomiendo dos películas en las que actúa el dúo humorístico británico formado por Simon Pegg y Nick Frost: Shaun of the dead y Hot Fuzz (parte de la trilogía Cornetto).

Con esta película podemos adentrarnos en el round 3 (y último por el momento) de las batallas de Maxwell para defender las ecuaciones de sus sueños. Y esta batalla será contra la mecánica cuántica. Las cuatro leyes empíricas detrás de las ecuaciones de Maxwell (asociadas a los experimentos de Coulomb, Ampère y Faraday, y a la inexistencia de monopolos magnéticos) son compatibles con observaciones y experimentos en escalas muy grandes y muy pequeñas. Por ejemplo, la ley de Coulomb es compatible con experimentos para separaciones entre cargas en distancias que van desde 10⁸ m hasta 10⁻¹⁶ m. En resumen, el comportamiento del mundo microscópico es compatible con las leyes detrás de las ecuaciones de Maxwell.

Sin embargo, el campo electromagnético clásico en las ecuaciones de Maxwell no está cuantizado. Pero eso no es un problema, las ecuaciones de Maxwell son las ecuaciones de onda para un fotón. Cuantizarlas cambia la interpretación física de los campos E y B, pero no agrega ni quita términos en las ecuaciones. La radiación de cuerpo negro, que corresponde a la emisión de fotones en equilibrio térmico por una fuente, satisface las ecuaciones de Maxwell tal como las vemos en esta materia.

La convivencia de Maxwell con la nueva física del siglo XX no fue lecho de rosas (para la nueva física). La ecuación de Schrödinger, como las ecuaciones de Newton, no es relativista. Es decir, la ecuación de Schrödinger es invariante de Galileo. Acoplar ciertos fenómenos cuánticos con el electromagnetismo no requirió modificar al electromagnetismo, sino modificar la mecánica cuántica para considerar el caso relativista. Nuevamente las ecuaciones de Maxwell resultaron victoriosas. Pero en la descripción cuántica-relativista las cosas se ponen difíciles. El número de partículas puede cambiar en el tiempo vía los procesos de creación y destrucción de pares: un fotón puede generar pares de partículas, siempre conservando la carga (como al crear un electrón y un positrón). La descripción de estos fenómenos es hoy descripta por la electrodinámica cuántica, que es la teoría que acopla correctamente al electromagnetismo y la materia en el caso cuántico-relativista. Esta teoría, por la que Sin-Itiro Tomonaga, Julian Schwinger y Richard Feynman ganaron el premio Nobel en 1965, es increíblemente precisa y compatible con todos los experimentos realizados hasta el momento. Y algunas propiedades que conocemos del electromagnetismo clásico, como el principio de superposición, se pierden: el hecho de que el número de partículas pueda cambiar permite que un fotón interactúe con otro fotón. Pero esto no es el resultado de una corrección a las ecuaciones de Maxwell, sino del acoplamiento de las ecuaciones de Maxwell con la cuántica (y con la materia). Los que quieran aprender más sobre esto, qué mejor que hacerlo escuchando a uno de los creadores de la teoría:

En resumen, las ecuaciones de Maxwell no cambiaron a lo largo del siglo XX, aún durante la revolución de la mecánica cuántica. Las ecuaciones que hoy conocemos para los fenómenos electromagnéticos son las mismas que Maxwell escribió en 1861. Y no son una aproximación clásica que requiera correcciones en el caso cuántico. Para un solo fotón en vacío, las ecuaciones de Maxwell siguen siendo las ecuaciones de la física compatibles con las observaciones experimentales.

Scott Pilgrim es un cómic canadiense creado por Bryan Lee O’Malley (también hay una película, pero eso será tema de un próximo post). El comic sigue las aventuras de Scott, que luego de enamorarse perdidamente de Ramona Flowers, descubre que la relación con Ramona tiene duras condiciones: debe enfrentarse con sus siete ex diabólicos (por diversos motivos, este tipo de cosas siempre se descubren demasiado tarde). Por enfrentarse, me refiero a que debe ganar una pelea. Y cada uno de los ex de Ramona es alguien famoso, fuerte, o con superpoderes. El cómic, que explora entre otras cosas las consecuencias de las relaciones tóxicas, combina el estilo del cómic norteamericano con el del manga y los videojuegos (por ejemplo, la banda de rock de Scott Pilgrim se llama “Sex Bob-omb”, una referencia a los Bob-omb de Super Mario).

James Maxwell también descubrió que para escribir las ecuaciones de sus sueños debía enfrentarse a varios ex malvados. Sus ecuaciones eran, y fueron, incompatibles con varias otras ecuaciones de la física. Maxwell no llegó a ver el final de varios de esos enfrentamientos, pero su teoría los ganó a todos. En más de un sentido sus ecuaciones son las primeras ecuaciones de la física contemporánea, que iniciaron (antes que la cuántica) una revolución que afectaría fuertemente a toda la física en la primera mitad del siglo XX. Y sus ecuaciones no cambiaron ni en un solo término, a pesar de todos los cambios que tuvo la física en ese período. Como Samwise Gamgee en El señor de los anillos, Maxwell tal vez sea el héroe anónimo de la física moderna, opacado por otros grandes nombres que se subieron a sus hombros para poder ver mas lejos.

El primer round de Maxwell contra los ex malvados (¡round 1!) fue nada más y nada menos que contra el mismísimo Isaac Newton. En 1861, las ecuaciones de Newton y su Principia Mathematica tenían 174 años sin que nadie se atreviese a discutir su validez. Pero la fuerza electromagnética tiene un problema. Para una carga puntual q en movimiento que se mueve con velocidad v, la fuerza electromagnética en unidades cgs-Gaussianas está dada por la fuerza de Lorentz (donde c es la velocidad de la luz):

Las leyes de Newton nos dicen que dos observadores que se mueven con velocidad constante uno respecto al otro deben medir la misma fuerza. Pero si un observador S’ se mueve con velocidad constante u respecto a nuestro sistema de referencia S, el observador S’ verá que la carga se mueve con una velocidad relativa v‘ = v - u. La igualdad de la fuerza para ambos observadores implica que si nosotros vemos campos eléctricos y magnéticos E y B, el observador S’ debe ver campos B‘ = B y E‘ = E – u x B/c. Pero las ecuaciones de Maxwell no son compatibles con esta transformación para los campos frente a una transformación de Galileo. Así, o las ecuaciones de Newton están mal, o las ecuaciones de Maxwell están mal. Alguien iba a salir lastimado de este enfrentamiento.

Como hoy sabemos, este round lo ganó Maxwell (¡Game over!). La teoría de la relatividad especial de Einstein modificó la mecánica clásica, e introdujo nuevas transformaciones frente a un cambio de sistema de referencia que preservan la invariancia de las ecuaciones de Maxwell. En 1905, las ecuaciones de Maxwell seguían siendo las mismas que las que Maxwell escribió en 1861. Las ecuaciones que fueron modificadas fueron las de la mecánica de Newton, no las del electromagnetismo. Más adelante en la materia veremos este problema, y su resolución, en detalle.

¡Round 2!: Hace un tiempo Juan Pablo Pinasco (@jpinasco) del Departamento de Matemática me mandó un paper muy interesante, con una hipotética demostración de las ecuaciones de Maxwell que contó alguna vez Feynman (¿a modo de broma?), y que Freeman Dyson formalizó y puso por escrito:

• Feynman’s proof of the Maxwell equations.

Feynman parte de las ecuaciones de Newton y las relaciones de conmutación en cuántica, y obtiene dos de las ecuaciones de Maxwell (Dyson considera que las otras dos ecuaciones de Maxwell meramente definen las fuentes). Pero son las otras dos ecuaciones (y la conservación de la carga en particular) las que hacen imposible sostener la invariancia de Galileo en el electromagnetismo. Como Dyson mismo comenta (y otros autores en sus cartas al editor en el mismo archivo, pueden encontrarlas a partir de la cuarta página), el argumento de Feynman debe ser interpretado, en lugar de como una demostración, más bien como una verificación de la consistencia de la física que conocemos. ¡Maxwell también gana este round!

Para cerrar este primer posteo con una temática más ligera que los posteos previos del ciclo de cine de terror e historia del electromagnetismo, les dejo un video con una versión animada del cómic de Scott Pilgrim:

En esta última entrega de la serie de películas de terror (¡por el momento!), tenemos una de las mejores de películas de John Carpenter. La cosa (The thing, 1982) cuenta la historia de un grupo de investigadores encerrados en una base norteamericana en la Antártida, que debe enfrentarse a un parásito extraterrestre. El parásito no se puede destruir, y se transforma en el organismo que invade (y más tarde puede transformarse en otras cosas). Es un clásico del cine de terror y de la ciencia ficción, y una película de culto que pueden ver en Netflix. No solo la película es fuertemente recomendada para aprobar esta materia, sino que la temática general (con personas aisladas y encerradas, y tests de sangre para detectar un virus) es ideal para los tiempos que vivimos.

El concepto de que “nada se pierde, todo se transforma” se basa en la observación de la naturaleza. Tal vez el primero en ponerlo en estos términos fue Antoine Lavoisier, en el marco de sus experimentos en química. Pero en física hoy conocemos formalmente esta idea en la forma de leyes de conservación: ciertas cantidades en la naturaleza no cambian aún si un sistema aislado evoluciona en el tiempo. James Clerk Maxwell fue el primero en notar que las expresiones empíricas que se seguían de las observaciones experimentales de Coulomb, Ampère y Faraday no conservaban la carga eléctrica: la carga eléctrica según las ecuaciones del electromagnetismo de la época podía ser creada o destruida de la nada. Pero la evidencia experimental hasta ese momento indicaba que la producción de una carga positiva venía siempre acompañada por una carga negativa, es decir, que la carga total en un sistema aislado no puede cambiar (algo que se sigue verificando experimentalmente hasta el día de hoy). Maxwell entonces modificó las expresiones agregando el famoso término de la corriente de desplazamiento, de forma tal que las ecuaciones del electromagnetismo conserven la carga eléctrica total:

Como vimos en clase, de izquierda a derecha y de arriba hacia abajo, estás ecuaciones se obtienen respectivamente de la fuerza de Coulomb, de los experimentos de Faraday (que Maxwell escribió en esta forma), de la no observación de cargas magnéticas, y de las observaciones de Ampère. El último término en esta ecuación fue agregado por Maxwell para conservar la carga. Y aquí aparece la genial Emmy Noether:

Uno de los teoremas más importantes en la física teórica moderna, el teorema de Noether, nos dice que cada ley de conservación está asociada a una simetría. ¿A qué simetría se asocia la conservación de la carga? Resulta que esta conservación está asociada a la simetría de gauge del electromagnetismo. Sabemos que, por ejemplo, podemos sumarle una constante C a cualquier potencial φ, y obtener el mismo campo eléctrico E:

Es decir, podemos elegir arbitrariamente el cero del potencial. Y también sabemos que el trabajo necesario para desplazar una carga q entre dos puntos 1 y 2 con diferentes valores del potencial es W = q(φ₂ – φ₁). Luego, si fuera posible crear cargas de la nada, el trabajo necesario para crear una carga en un punto cualquiera debería ser qφ. Pero esto nos permitiría determinar el valor absoluto del potencial electrostático φ (¡y determinar en forma absoluta el cero del potencial!) simplemente midiendo el trabajo necesario para crear la carga q. Así, la conservación de la carga y la libertad de gauge del electromagnetismo están relacionadas: si la carga total no se conserva, podemos determinar en forma única el cero de los potenciales.

La conservación de la carga implica que no podemos cambiar la cantidad total de carga en el universo. Pero esto no implica que el universo tenga una carga eléctrica total igual a cero. Podría haberse originado con un desbalance de carga (por ejemplo, más cargas positivas que negativas), y por la conservación de la carga, el desbalance total de carga hoy debería ser el mismo que al inicio del universo. Pero toda la evidencia observacional hasta el momento indica que el universo es eléctricamente neutro. Por ejemplo, un desbalance de carga generaría campos eléctricos que impondrían una dirección privilegiada en el espacio y una anisotropía en la radiación cósmica de fondo, o una anisotropía en los rayos cósmicos que llegan a la Tierra. Nada de eso se observa. Si hay un desbalance de carga en el universo, debe ser muy pequeño.