Hoy viernes, de 16 a 18, pueden pasar por la oficina de Florencia (2144). Si no, pueden recurrir a la ayuda de nuestros representantes virtuales en el Campus. Importantes novedades, aquí mismo, más tarde.

Finalmente, las notas de la clase práctica del lunes quedaron pasadas en limpio. Pueden bajarlas [aquí] (las actualizamos con un breve comentario que se publicó en el Campus). En el límite de infinitas iteraciones, la red de este ejemplo es un fractal de dimensión igual a 2. Miren la figura del post anterior. La red completa puede subdividirse en cuatro subredes autosemejantes a la red original. Si se duplica el tamaño de estas subredes, se obtiene la red original. Es lo mismo que pasa con un cuadrado bidimensional. Si se divide al cuadrado en cuatro cuadrados de lado mitad, el cuadrado original puede obtenerse duplicando el tamaño de cualquiera de los cuadrados pequeños. En general, si un conjunto puede dividirse en N partes iguales autosemejantes al conjunto original, y el factor de escala es S, la dimensión D del conjunto es tal que

El triángulo de Sierpinski es un ejemplo de fractal de dimensión no entera. Apliquen la fórmula anterior y calculen su dimensión fractal.

La clase práctica de ayer, resolvimos un problema del libro de Pathria y Beale. Es el último problema del capítulo 14, pero no por ser el último es el más difícil. En realidad, no tiene ninguna cuenta complicada.

No hay (todavía) un apunte de clase, pero pueden ver [aquí] la presentación en pdf que usé ayer. Con esto tenemos una nueva familia de problemas para el parcial; ya veníamos repitiendo mucho.

Hemos empezado a corregir sus TP de Ising. Desde el momento en el que reciban el trabajo observado, van a tener una semana para enviar las correcciones.

Mañana hay clase de consulta desde las 17.

Mientras seguimos a la espera de sus prácticas computacionales, les recuerdo que las dos clases prácticas que tuvimos esta semana fueron muy importantes. El lunes vimos el grupo de renormalización aplicado a la cadena lineal. [Aquí] pueden bajar las notas de clase del cuatrimestre pasado. Encuentran este problema en la mayoría de los libros; miren, por ejemplo, los libros de Pathria y Beale, de Huang, de Dalvit et al.

El miércoles vimos la aproximación de Migdal-Kadanoff para la transformación del grupo de renormalización de la red cuadrada. [Aquí] pueden bajar la presentación de Bernardo, preparada para ver en pantalla completa; [aquí] pueden bajar las notas del cuatrimestre pasado. Es fácil inventar problemas parecidos con otras redes.

El lunes hay clase de práctica normal. El miércoles habrá clase de consultas desde las 17. El parcial es el lunes 8, con el mismo protocolo que el primer parcial. Estén atentos al viernes que viene, porque vamos a dar algunas palabras clave sobre los problemas. Previsiblemente, habrá un problema de fermiones, otro de bosones y uno que combine renormalización con Ising. En 2019, tomamos dos problemas de esta clase (parcial, recuperatorio). Con eso agotamos nuestra imaginación. El cuatrimestre pasado hubo un problema con una cadena decorada. Si quieren un problema nuevo de este tipo, tomen el problema de la escalera de Ising e inserten espines en el medio de todos los enlaces. La suma sobre esos espines puede hacerse explícitamente; encuentren la constante de acoplamiento renormalizada.

La clase práctica del miércoles pasado, vimos la relación entre la energía libre de Landau y la energía libre de Gibbs en la aproximación de Bragg-Williams para el modelo de Ising. Es decir, vimos un ejemplo concreto en donde la energía libre de Landau aparece naturalmente, y no como un artefacto a medida para explicar de manera fenomenológica las transiciones de fase. De nuevo vimos la importancia de tomar el límite termodinámico, sin el cual no habría ninguna singularidad a temperatura finita. En relación con esto, la animación de abajo muestra el valor medio del espín en función del campo externo para una temperatura mayor a la crítica, pero para un número finito de espines. Sólo tiene sentido hablar de magnetización espontánea cuando N tiende a infinito.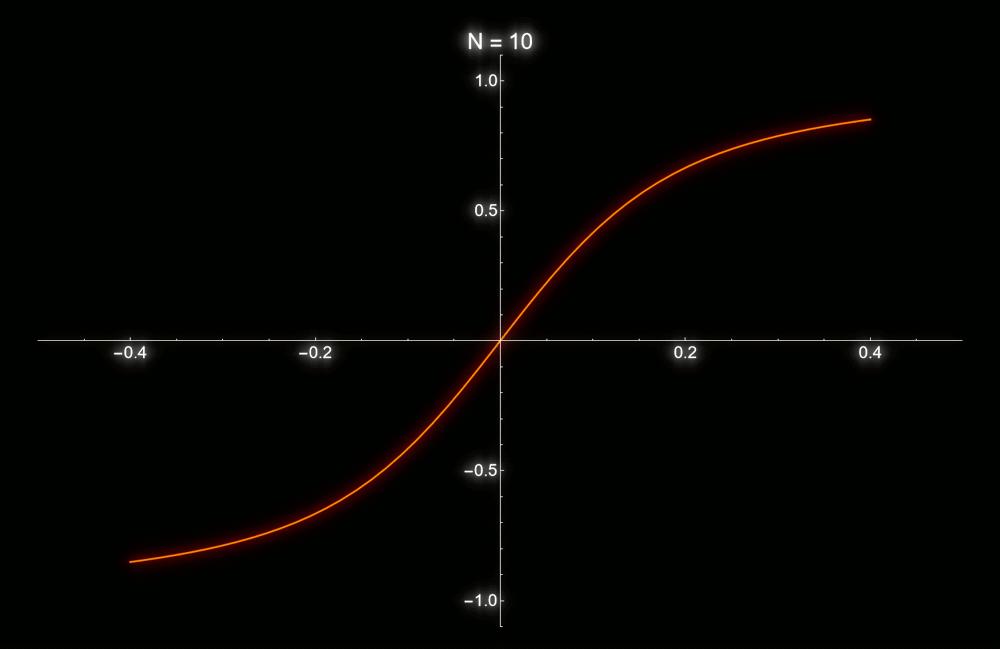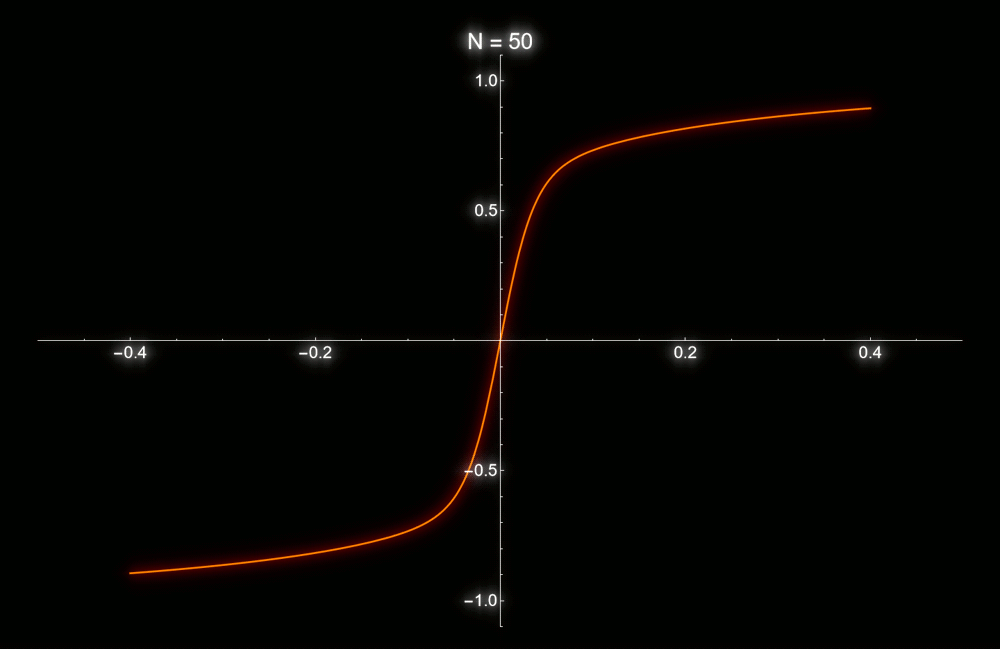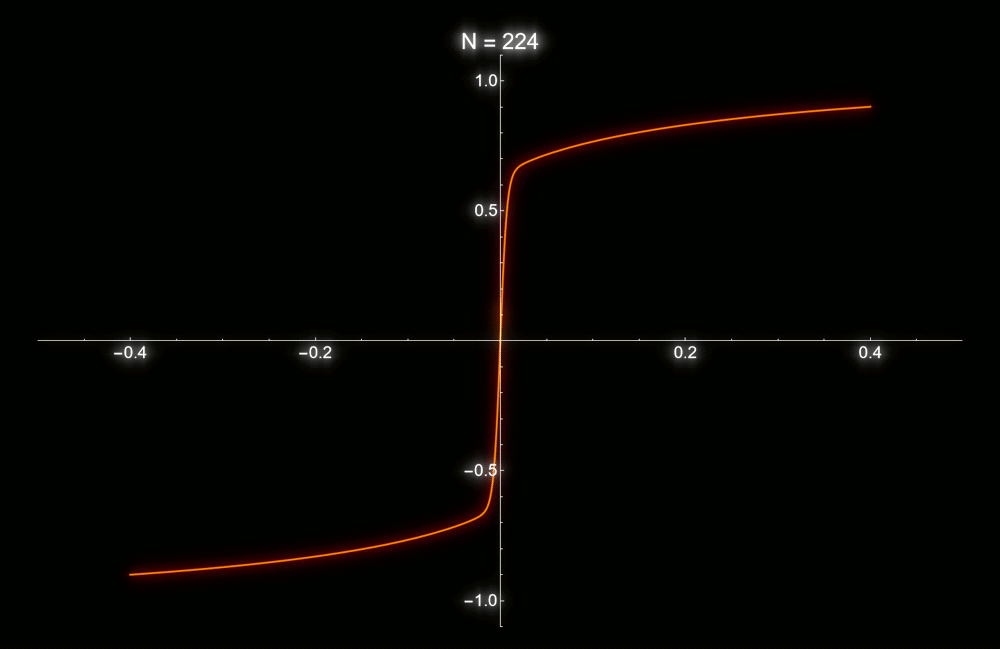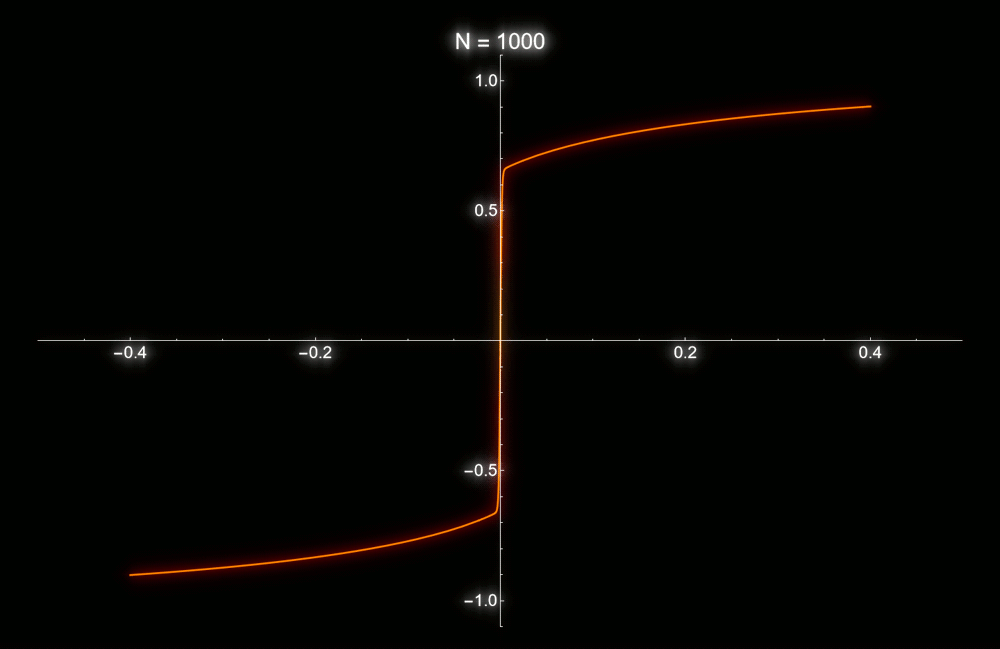 

[Aquí] pueden bajar las notas de clase, que corresponden al estreno mundial del problema 1 de la Guía 8, que sienta un precedente de ítem r.  [Aquí] pueden bajar la Guía 8.

Supongo que están muy concentrados en el trabajo computacional, así que no los molesto más.

Les acabo de enviar un mail a todos con un link a una planilla para que anoten los grupos de la práctica computacional. Traten de resolver eso cuanto antes, así empiezan a trabajar. Hay una columna para los que están sin grupo. Si se organizan entre ustedes, mejor. Si no, veo cómo distribuir a los que quedaron sin grupo.

Para la práctica computacional, tienen que completar el notebook de Python que pueden encontrar [aquí]. Para los que no tienen la menor idea de Python, es recomendable que lean los siguientes tutoriales preparados por la FIFA (Federación Interestudiantil de Físicos Argentinos):

• Introducción
• Numérico y Laboratorio

Aprovechen las herramientas de AI para generar código.

Para poder usar el notebook sin necesidad de tener Python instalado en sus computadoras, deben tener una cuenta de Google y bajarse la aplicación de Google Colaboratory. Hagan una copia del notebook en su propio drive. Después deberán compartirnos el enlace con el notebook completo.

La entrega consiste en el notebook de Python con los algoritmos completos y los resultados. La fecha límite de entrega es el  26 de junio a las 23:59, según el reloj de mi videocasetera. Envíennos el link a los cinco docentes de la práctica.

Formen grupos de tres personas, eventualmente de 2 y de 4. Si alguien no consiguió asociarse, comuníquense por mail conmigo y los pongo en contacto.

Cuando tengan el notebook funcionando, divídanse el trabajo para aprovechar el tiempo de computadora. De manera realista, tienen que poder hacer todo en menos de una semana a un ritmo tranquilo. Hay casi dos semanas entre la fecha de entrega y el segundo parcial. Aprovechen esta semana para hacer la práctica computacional. Después de hoy, no vamos a tener prácticas hasta el 24

[Aquí] pueden bajar las notas de clase de la práctica de ayer, con las decepcionantes aproximaciones de campo medio de complejidad creciente y mejoras minúsculas. Decepcionantes en ese sentido. El solo hecho de predecir magnetización espontánea es un paso fundamental. Fundamental en ese sentido, pero decepcionante en el sentido de que no obtuvimos la transición de fase como una singularidad en las funciones termodinámicas, a través de la función de partición y del límite termodinámico, sino de una manera más bien ad hoc.

El miércoles pasado mostramos en la clase de práctica algo que resultó novedoso para muchos: la multiplicación de matrices sin usar dibujitos. Eso no debería haber sucedido. [Aquí] pueden bajar las notas de clase, con los problemas que resolvimos de la Guía 7. El método de la matriz de transferencia es muy poderoso, en especial la idea de que el límite termodinámico está dominado por el mayor autovalor de una cierta matriz.

La Guía 7, acerca del modelo de Ising, puede bajarse [aquí]. Por más que intentamos, no conseguimos ningún problema donde hubiera que calcular integrales.