Técnicamente, como aún no son las 22,  todavía estamos en clase. Les dejo un breve apunte que sigue más o menos lo que hicimos durante la clase de hoy. Lo pueden bajar [aquí]. Con lo que han visto, pueden resolver casi todas las cuestiones del problema 1 y hacer (en parte rehacer) los problemas del 6 al 10. Empiecen con el pie derecho y no se atrasen con los problemas. Consulten ahora y no en el parcial.

El enunciado del primer parcial puede bajarse [aquí]. El resuelto, [aquí]. Ya que es poco probable que hoy tengan consultas sobre cuerpo rígido, aprovechen para consultar sobre el parcial. En la imagen, el sistema del problema 1 encerrado en una trampa cuadrada.

Con esta emoción recibimos a la guía de cuerpo rígido. Para bajar [aquí].

Les recordamos que el primer parcial es este jueves 18/5 a las 17 horas en el aula 6 del Pabellón 2.

Una entrada del curso del año pasado. Es en relación al problema 9 de la Guía 3, que es el movimiento en el potencial central que resulta de sumarle al potencial de Kepler un término centrífugo. Se muestra, entre otras cosas, cómo cambia la órbita de la partícula a medida que aumenta la perturbación.

• Primero, cómo cambia la órbita de una partícula en el potencial atractivo de Kepler, perturbado con un potencial U = k/r^2. La animación empieza en k = 0 y va subiendo, haciendo algunas pausas en órbitas que resultan cerradas. Link en la imagen.
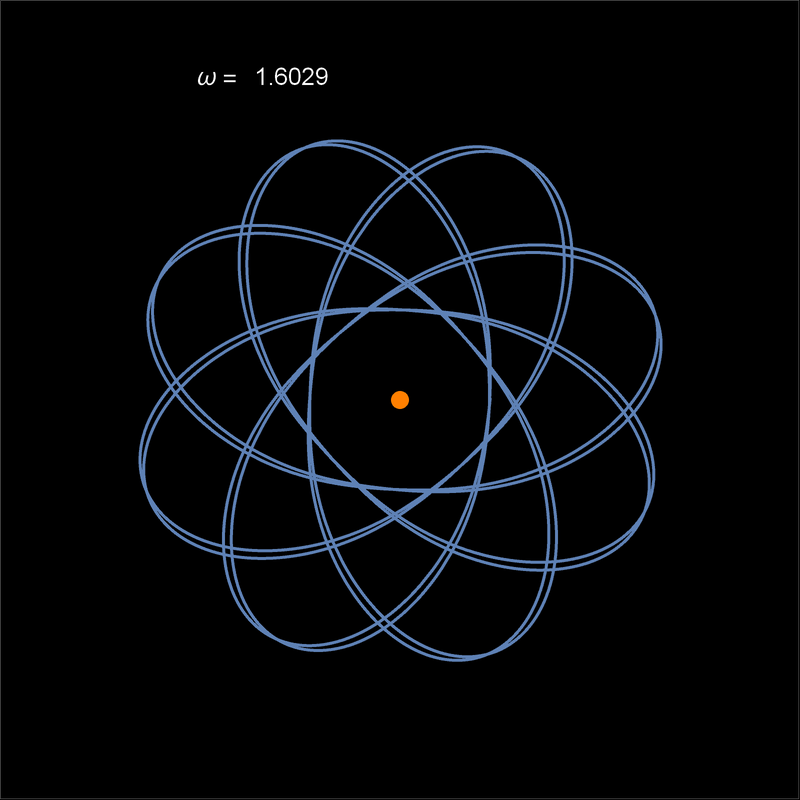
• La siguiente animación muestra la precesión en al caso de una perturbación pequeña con k > 0. La precesión es retrógrada. La elipse en rojo es la que corresponde instantáneamente al potencial sin perturbar. Notar que la elipse no rota a una velocidad uniforme. La velocidad de precesión se define a partir del movimiento del periapsis.
  
• La siguiente animación muestra la precesión en al caso de una perturbación pequeña con k < 0. La precesión es prógrada.
• Cuando la perturbación es grande, ya no puede hablarse de una elipse que rota; se dice que la órbita tiene forma de roseta.