Author Archives: Juan Zanella
Guía 6
Con esta emoción recibimos a la guía de cuerpo rígido. Para bajar [aquí].
Primer parcial
El Kepler de la navidad pasada
Una entrada del curso del año pasado. Es en relación al problema 9 de la Guía 3, que es el movimiento en el potencial central que resulta de sumarle al potencial de Kepler un término centrífugo. Se muestra, entre otras cosas, cómo cambia la órbita de la partícula a medida que aumenta la perturbación.
- Primero, cómo cambia la órbita de una partícula en el potencial atractivo de Kepler, perturbado con un potencial U = k/r^2. La animación empieza en k = 0 y va subiendo, haciendo algunas pausas en órbitas que resultan cerradas. Link en la imagen.
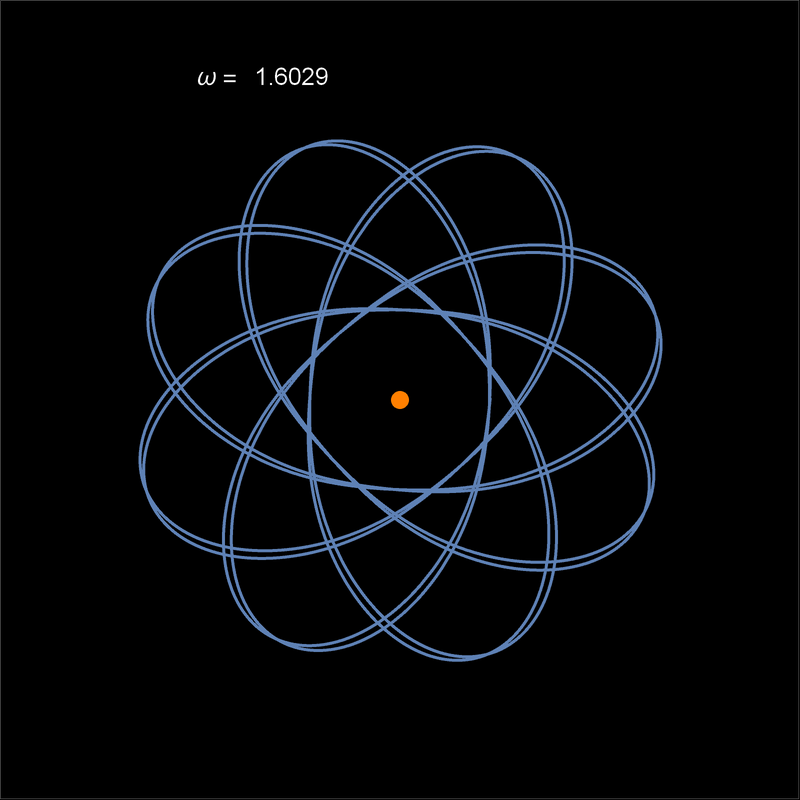
- La siguiente animación muestra la precesión en al caso de una perturbación pequeña con k > 0. La precesión es retrógrada. La elipse en rojo es la que corresponde instantáneamente al potencial sin perturbar. Notar que la elipse no rota a una velocidad uniforme. La velocidad de precesión se define a partir del movimiento del periapsis.
- La siguiente animación muestra la precesión en al caso de una perturbación pequeña con k < 0. La precesión es prógrada.
- Cuando la perturbación es grande, ya no puede hablarse de una elipse que rota; se dice que la órbita tiene forma de roseta.
¿Existen los lagrangianos?
Un paper para leer en un ratito y muy por arriba, y un buen ejemplo de que uno nunca puede estar seguro de tener la última palabra. Link en la imagen. 
El tema principal es de larga fama y se conoce como el problema inverso del cálculo variacional: dado un sistema de ecuaciones diferenciales, ¿existe un lagrangiano que las genere? No en todos los casos…quizá.
Cosas cayendo en lugares
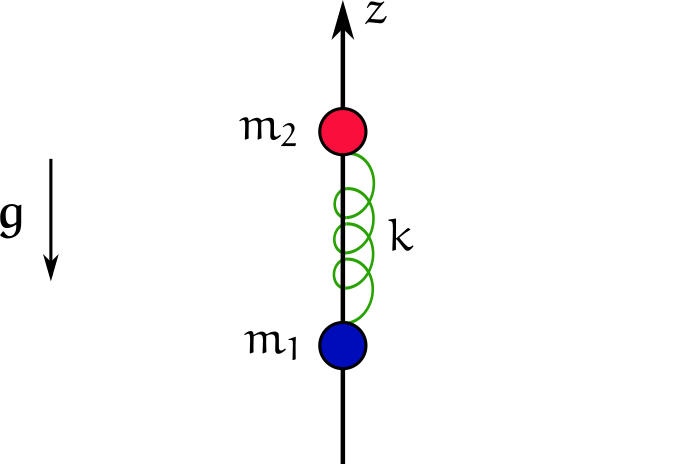
Recordarán el problema 11 de la Guía 1. Eran dos partículas unidas por un resorte en caída libre en un campo gravitatorio uniforme.
Si Z es la posición relativa de las partículas y μ es la masa reducida, la evolución de Z está dada por ![]() Cuando se les pregunta en el enunciado por el rol de g en esta ecuación, la respuesta es: “ninguno”. Este resultado es general: un sistema de partículas en caída libre en un campo gravitatorio uniforme, observado desde un sistema que también está en caída libre, se comporta exactamente como si estuviera en un sistema inercial sin ningún campo gravitatorio externo. Esto sirve para hacer experimentos en gravedad cero sin tener que alejarse infinitamente de cualquier cuerpo masivo. Alcanza, por ejemplo, con construir una torre hueca muy alta, hacer vacío en su interior, construir el experimento dentro de una cápsula y dejar caer la cápsula desde lo alto de la torre. Eso es lo que hacen, con alguna variación, en la Torre de Caída de Bremen, en Alemania.
Cuando se les pregunta en el enunciado por el rol de g en esta ecuación, la respuesta es: “ninguno”. Este resultado es general: un sistema de partículas en caída libre en un campo gravitatorio uniforme, observado desde un sistema que también está en caída libre, se comporta exactamente como si estuviera en un sistema inercial sin ningún campo gravitatorio externo. Esto sirve para hacer experimentos en gravedad cero sin tener que alejarse infinitamente de cualquier cuerpo masivo. Alcanza, por ejemplo, con construir una torre hueca muy alta, hacer vacío en su interior, construir el experimento dentro de una cápsula y dejar caer la cápsula desde lo alto de la torre. Eso es lo que hacen, con alguna variación, en la Torre de Caída de Bremen, en Alemania.  Para duplicar el tiempo que pueden durar los experimentos, que de todas formas es de unos pocos segundos, en lugar de dejar caer la cápsula desde lo alto, la arrojan hacia arriba desde el fondo: también es posible subir en caída libre. [Aquí] pueden ver un interesante video (tiene subtítulos en inglés).
Para duplicar el tiempo que pueden durar los experimentos, que de todas formas es de unos pocos segundos, en lugar de dejar caer la cápsula desde lo alto, la arrojan hacia arriba desde el fondo: también es posible subir en caída libre. [Aquí] pueden ver un interesante video (tiene subtítulos en inglés).
La clase pasada vimos la precesión relativista de Mercurio, que es lo mejor que puede conseguirse en el sistema solar. En el transcurso de un siglo, las correcciones relativistas hacen que el perihelio de Mercurio avance unos 43 segundos de arco extra. Lo más asombroso, quizá, es que ese número ya se conociera, segundos de arco más, segundos de arco menos, en 1859. En el centro de la galaxia hay un agujero negro supermasivo, llamado Sagitario A*. Para algunas de las estrellas que orbitan ese agujero negro, los efectos relativistas son miles de veces mayores que para el pobre Mercurio. En el año 2020 se publicó la primera medición de la precesión de una de esas estrellas, llamada S2, con un período de revolución de 16 años. En un solo período de revolución, la precesión del periapsis de S2 es de 12 minutos de arco. La siguiente figura está tomada del artículo de la Wikipedia acerca del cúmulo de estrellas Sagitario A*, y muestra las órbitas de algunas de las estrellas.
Abajo, un video que muestra algunas de las estrellas durante 20 años de observaciones (link en la imagen a la fuente).
Otro video muy impresionante, pero completamente newtoniano, es el de cuatro exoplanetas alrededor de la estrella HR 8799.
Hechos inquietantes 6, o quizá 7
 Si siguieron el argumento del problema 13 de la Guía 2, que también pueden leer directamente en el libro de Landau y Lifshitz, sabrán que un sistema aislado con n grados de libertad tiene 2n -1 integrales de movimiento. Esto es, 2n - 1 constantes de movimiento que no dependen explícitamente del tiempo.Que el sistema sea aislado significa que su lagrangiano no depende explícitamente del tiempo.
Si siguieron el argumento del problema 13 de la Guía 2, que también pueden leer directamente en el libro de Landau y Lifshitz, sabrán que un sistema aislado con n grados de libertad tiene 2n -1 integrales de movimiento. Esto es, 2n - 1 constantes de movimiento que no dependen explícitamente del tiempo.Que el sistema sea aislado significa que su lagrangiano no depende explícitamente del tiempo.
Si miran a mi derecha, notarán un sistema de una partícula libre moviéndose en un plano. Tiene dos grados de libertad y por lo tanto tres integrales de movimiento. Si miran a mi izquierda, verán un sistema con otra partícula libre moviéndose en otro plano. Considerado separadamente, este sistema también tiene tres integrales de movimiento. Tres por un lado, tres por el otro, en total hay seis integrales de movimiento. Pero supongan ahora que considero a los dos sistemas en conjunto. Las partículas siguen siendo partículas libres, pero ahora el sistema tiene cuatro grados de libertad y, por lo tanto, existen siete integrales de movimiento. ¿De dónde salió la integral de movimiento que sobra?
Simetrías
 Debido a lo accidentado de la clase del lunes, pasé en limpio los problemas que pensaba explicar y agregué también el problema de la integral de Jacobi y unas notas acerca del método “a la Landau” que se menciona en los problemas de la Guía 2. Para bajar [aquí].
Debido a lo accidentado de la clase del lunes, pasé en limpio los problemas que pensaba explicar y agregué también el problema de la integral de Jacobi y unas notas acerca del método “a la Landau” que se menciona en los problemas de la Guía 2. Para bajar [aquí].
También les traigo citas:
¿Habrá cosa que se parezca menos a la belleza que la simetría perfecta? (No quiero hacer una apología del caos; entiendo que en todas las artes nada suele agradar como las simetrías imperfectas…)
Borges, en Textos Cautivos.
Así, pues, nuestro problema es explicar de d6nde proviene la simetría. ¿Por qué la naturaleza es tan casi simétrica? Nadie tiene una idea de por qué. Lo único que podemos sugerir es algo como esto: Hay una puerta en Japón, en Neiko, que los japoneses llaman algunas veces la puerta más hermosa de todo Japón; se construyó en una época en que había una gran influencia del arte chino. Esta puerta es muy ornamentada, con muchos tímpanos y hermosas estatuas y columnas y cabezas de dragones y príncipes esculpidos en los pilares, etc. Pero cuando se mira de cerca se ve que en el dibujo elaborado y complejo de uno de los pilares, uno de los pequeños elementos de diseño está esculpido cabeza abajo…
Feynman, en Física, vol. I.
Babel
Hechos inquietantes 5
Esta vez en el Campus, en relación a los problemas 16 y 17 de la Guía 1. Link [aquí].