La remozada Guía 8 puede bajarse [aquí]. Por remozada queremos decir que le cambiamos el tipo de letra. Con el tipo de letra, también le cambiamos las letras. Y con las letras, los problemas. Contiene una sola integral terrible. Bueno, dos.

Category Archives: Novedades
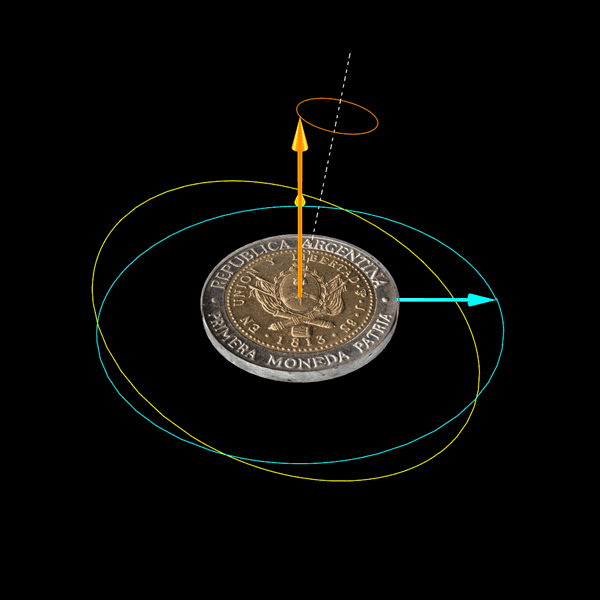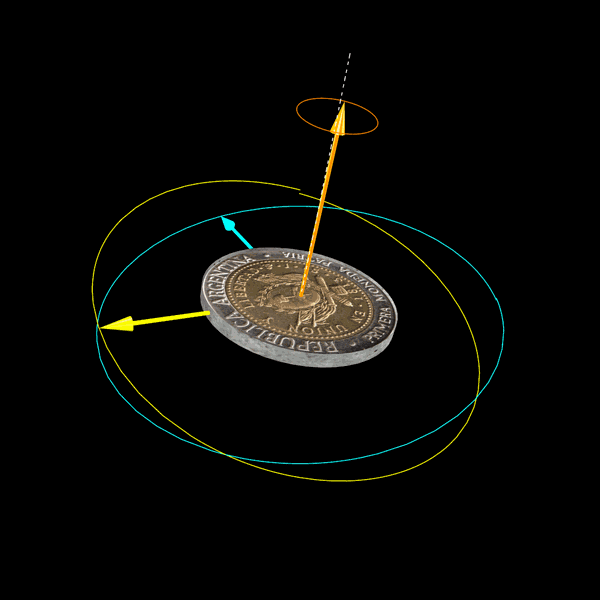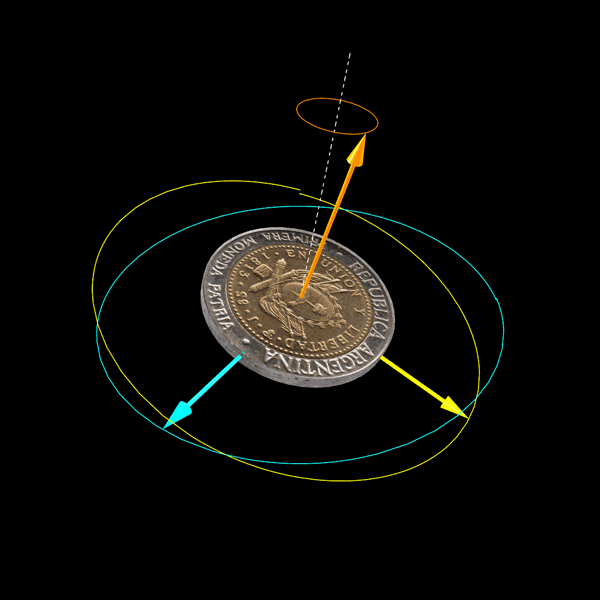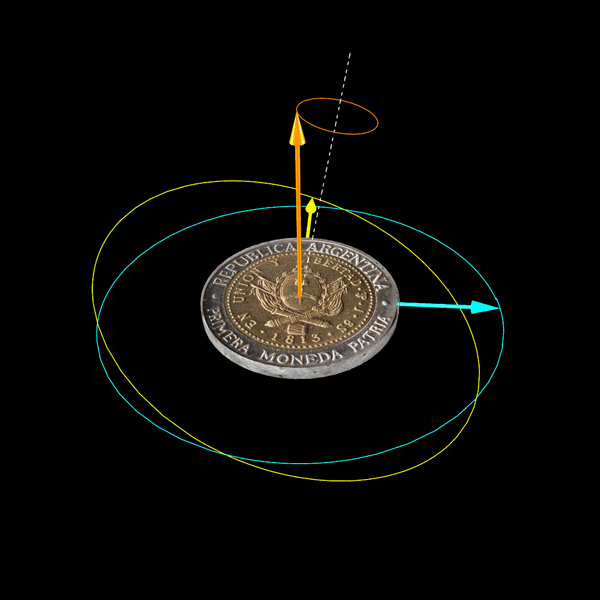
Guía 6. Problema 22.
Esto es lo que hace el giróscopo del problema 22 de la Guía 6.
 No sólo las condiciones iniciales están elegidas para que el problema pueda integrarse en términos de funciones elementales, sino que la solución es fácil de interpretar. Deberían ver en sus soluciones que el giróscopo hace lo que muestra la animación anterior. El problema 22 guarda una gran analogía con el problema 19.
No sólo las condiciones iniciales están elegidas para que el problema pueda integrarse en términos de funciones elementales, sino que la solución es fácil de interpretar. Deberían ver en sus soluciones que el giróscopo hace lo que muestra la animación anterior. El problema 22 guarda una gran analogía con el problema 19.
Una cuestión interesante es de dónde viene el giróscopo para llegar a esa condición inicial. Si propagamos la solución hacia los tiempos negativos, vemos que el giróscopo viene de la misma posición asintótica hacia la que tiende en el futuro. Abajo hay una animación entre -T y T, con T suficientemente grande para ver el comportamiento asintótico hacia el pasado y hacia el futuro.
Inestabilidad del eje intermedio
Abajo hay un video que muestra la inestabilidad del eje intermedio en la Estación Espacial Internacional. Link en la imagen.
En la guía sólo se pide demostrar la estabilidad o la inestabilidad. Pero el movimiento puede determinarse exactamente por cuadraturas usando cierta clase de funciones. Está hecho en la sección 37 del libro de Landau y Lifshitz. [Aquí] hay un paper más detallado. En [este] video está explicado más gráficamente y a nivel del público general. Ahí se plantea la siguiente pregunta inquietante: ¿podría estar la Tierra rotando alrededor del eje intermedio y en cualquier momento quedamos todos patas para arriba? En el video está dicho de manera más técnica. Goldstein menciona el problema en el contexto de los satélites artificiales, en la sección 5-6, en una nota a pie de página que empieza como “If there are dissipative mechanisms present, these stability arguments have to be modified…” Al menos en mis ediciones, está en la página 210 de la segunda y en la 205 de la tercera. En la versión en español, la nota empieza diciendo “Cuando haya mecanismos disipativos, habrá que modificar estos razonamientos acerca de la estabilidad”, y está en la página 267. Ya lo he dicho antes: es muy buena la versión del libro de Goldstein en español.
En el post anterior, en el minuto 6:40 del video, se ve un trompo que se da vuelta. Es el ["Tippe top"]. Al contrario del fenómeno del eje intermedio, el comportamiento de este trompo depende de que haya torques externos. Abajo, una fotografía muy famosa de Pauli y Bohr jugando con un Tippe top.

Trompos del mundo, uníos
Clase práctica del jueves 1/6 [actualizado y re actualizado]
Para que no tengan urgencia en copiar del pizarrón, [aquí] les dejo el guion de la clase de hoy, que va a tratar acerca del disco de Feynman. Es una versión preliminar. Mañana viernes subo una versión actualizada. Edit: actualizado. [Aquí] pueden leer lo que dice Feynman en su autobiografía. [Aquí], una traducción.
Tecnicismos
Técnicamente, como aún no son las 22, todavía estamos en clase. Les dejo un breve apunte que sigue más o menos lo que hicimos durante la clase de hoy. Lo pueden bajar [aquí]. Con lo que han visto, pueden resolver casi todas las cuestiones del problema 1 y hacer (en parte rehacer) los problemas del 6 al 10. Empiecen con el pie derecho y no se atrasen con los problemas. Consulten ahora y no en el parcial.
Primer parcial resuelto
Guía 6
Con esta emoción recibimos a la guía de cuerpo rígido. Para bajar [aquí].
Primer parcial
El Kepler de la navidad pasada
Una entrada del curso del año pasado. Es en relación al problema 9 de la Guía 3, que es el movimiento en el potencial central que resulta de sumarle al potencial de Kepler un término centrífugo. Se muestra, entre otras cosas, cómo cambia la órbita de la partícula a medida que aumenta la perturbación.
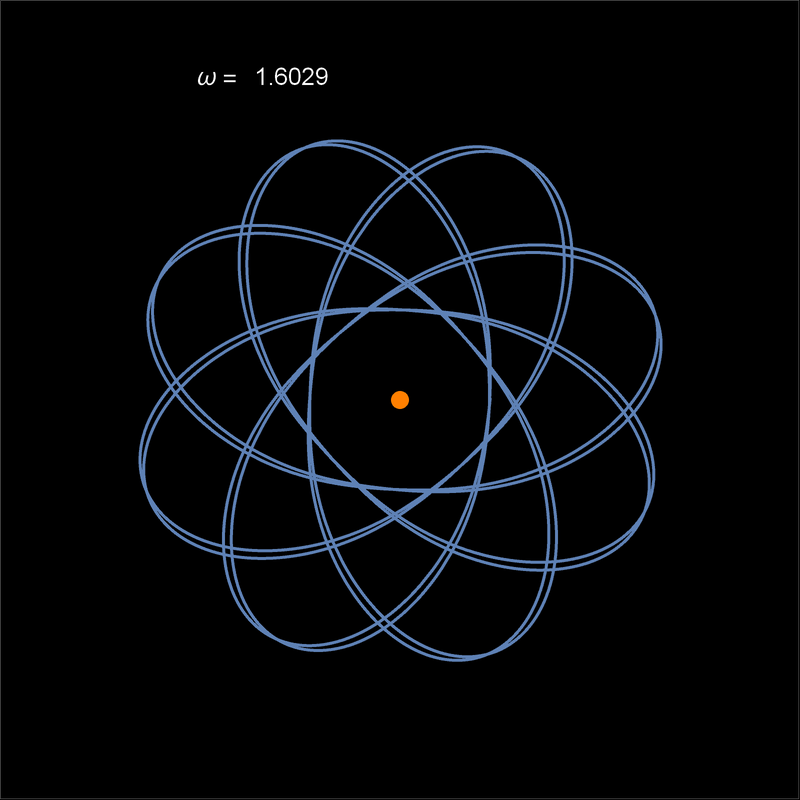
- Primero, cómo cambia la órbita de una partícula en el potencial atractivo de Kepler, perturbado con un potencial U = k/r^2. La animación empieza en k = 0 y va subiendo, haciendo algunas pausas en órbitas que resultan cerradas. Link en la imagen.
- La siguiente animación muestra la precesión en al caso de una perturbación pequeña con k > 0. La precesión es retrógrada. La elipse en rojo es la que corresponde instantáneamente al potencial sin perturbar. Notar que la elipse no rota a una velocidad uniforme. La velocidad de precesión se define a partir del movimiento del periapsis.
- La siguiente animación muestra la precesión en al caso de una perturbación pequeña con k < 0. La precesión es prógrada.
- Cuando la perturbación es grande, ya no puede hablarse de una elipse que rota; se dice que la órbita tiene forma de roseta.