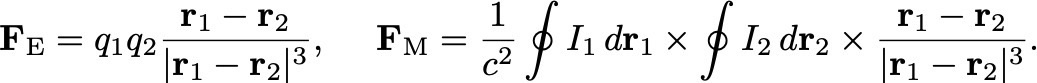Scott Pilgrim es un cómic canadiense creado por Bryan Lee O’Malley (también hay una película, pero eso será tema de un próximo post). El comic sigue las aventuras de Scott, que luego de enamorarse perdidamente de Ramona Flowers, descubre que la relación con Ramona tiene duras condiciones: debe enfrentarse con sus siete ex diabólicos (por diversos motivos, este tipo de cosas siempre se descubren demasiado tarde). Por enfrentarse, me refiero a que debe ganar una pelea. Y cada uno de los ex de Ramona es alguien famoso, fuerte, o con superpoderes. El cómic, que explora entre otras cosas las consecuencias de las relaciones tóxicas, combina el estilo del cómic norteamericano con el del manga y los videojuegos (por ejemplo, la banda de rock de Scott Pilgrim se llama “Sex Bob-omb”, una referencia a los Bob-omb de Super Mario).

James Maxwell también descubrió que para escribir las ecuaciones de sus sueños debía enfrentarse a varios ex malvados. Sus ecuaciones eran, y fueron, incompatibles con varias otras ecuaciones de la física. Maxwell no llegó a ver el final de varios de esos enfrentamientos, pero su teoría los ganó a todos. En más de un sentido sus ecuaciones son las primeras ecuaciones de la física contemporánea, que iniciaron (antes que la cuántica) una revolución que afectaría fuertemente a toda la física en la primera mitad del siglo XX. Y sus ecuaciones no cambiaron ni en un solo término, a pesar de todos los cambios que tuvo la física en ese período. Como Samwise Gamgee en El señor de los anillos, Maxwell tal vez sea el héroe anónimo de la física moderna, opacado por otros grandes nombres que se subieron a sus hombros para poder ver mas lejos.

El primer round de Maxwell contra los ex malvados (¡round 1!) fue nada más y nada menos que contra el mismísimo Isaac Newton. En 1861, las ecuaciones de Newton y su Principia Mathematica tenían 174 años sin que nadie se atreviese a discutir su validez. Pero la fuerza electromagnética tiene un problema. Para una carga puntual q en movimiento que se mueve con velocidad v, la fuerza electromagnética en unidades cgs-Gaussianas está dada por la fuerza de Lorentz (donde c es la velocidad de la luz):

Las leyes de Newton nos dicen que dos observadores que se mueven con velocidad constante uno respecto al otro deben medir la misma fuerza. Pero si un observador S’ se mueve con velocidad constante u respecto a nuestro sistema de referencia S, el observador S’ verá que la carga se mueve con una velocidad relativa v‘ = v - u. La igualdad de la fuerza para ambos observadores implica que si nosotros vemos campos eléctricos y magnéticos E y B, el observador S’ debe ver campos B‘ = B y E‘ = E – u x B/c. Pero las ecuaciones de Maxwell no son compatibles con esta transformación para los campos frente a una transformación de Galileo. Así, o las ecuaciones de Newton están mal, o las ecuaciones de Maxwell están mal. Alguien iba a salir lastimado de este enfrentamiento.

Como hoy sabemos, este round lo ganó Maxwell (¡Game over!). La teoría de la relatividad especial de Einstein modificó la mecánica clásica, e introdujo nuevas transformaciones frente a un cambio de sistema de referencia que preservan la invariancia de las ecuaciones de Maxwell. En 1905, las ecuaciones de Maxwell seguían siendo las mismas que las que Maxwell escribió en 1861. Las ecuaciones que fueron modificadas fueron las de la mecánica de Newton, no las del electromagnetismo. Más adelante en la materia veremos este problema, y su resolución, en detalle.

¡Round 2!: Hace un tiempo Juan Pablo Pinasco (@jpinasco) del Departamento de Matemática me mandó un paper muy interesante, con una hipotética demostración de las ecuaciones de Maxwell que contó alguna vez Feynman (¿a modo de broma?), y que Freeman Dyson formalizó y puso por escrito:

• Feynman’s proof of the Maxwell equations.

Feynman parte de las ecuaciones de Newton y las relaciones de conmutación en cuántica, y obtiene dos de las ecuaciones de Maxwell (Dyson considera que las otras dos ecuaciones de Maxwell meramente definen las fuentes). Pero son las otras dos ecuaciones (y la conservación de la carga en particular) las que hacen imposible sostener la invariancia de Galileo en el electromagnetismo. Como Dyson mismo comenta (y otros autores en sus cartas al editor en el mismo archivo, pueden encontrarlas a partir de la cuarta página), el argumento de Feynman debe ser interpretado, en lugar de como una demostración, más bien como una verificación de la consistencia de la física que conocemos. ¡Maxwell también gana este round!

Para cerrar este primer posteo con una temática más ligera que los posteos previos del ciclo de cine de terror e historia del electromagnetismo, les dejo un video con una versión animada del cómic de Scott Pilgrim:

En esta última entrega de la serie de películas de terror (¡por el momento!), tenemos una de las mejores de películas de John Carpenter. La cosa (The thing, 1982) cuenta la historia de un grupo de investigadores encerrados en una base norteamericana en la Antártida, que debe enfrentarse a un parásito extraterrestre. El parásito no se puede destruir, y se transforma en el organismo que invade (y más tarde puede transformarse en otras cosas). Es un clásico del cine de terror y de la ciencia ficción, y una película de culto que pueden ver en Netflix. No solo la película es fuertemente recomendada para aprobar esta materia, sino que la temática general (con personas aisladas y encerradas, y tests de sangre para detectar un virus) es ideal para los tiempos que vivimos.

El concepto de que “nada se pierde, todo se transforma” se basa en la observación de la naturaleza. Tal vez el primero en ponerlo en estos términos fue Antoine Lavoisier, en el marco de sus experimentos en química. Pero en física hoy conocemos formalmente esta idea en la forma de leyes de conservación: ciertas cantidades en la naturaleza no cambian aún si un sistema aislado evoluciona en el tiempo. James Clerk Maxwell fue el primero en notar que las expresiones empíricas que se seguían de las observaciones experimentales de Coulomb, Ampère y Faraday no conservaban la carga eléctrica: la carga eléctrica según las ecuaciones del electromagnetismo de la época podía ser creada o destruida de la nada. Pero la evidencia experimental hasta ese momento indicaba que la producción de una carga positiva venía siempre acompañada por una carga negativa, es decir, que la carga total en un sistema aislado no puede cambiar (algo que se sigue verificando experimentalmente hasta el día de hoy). Maxwell entonces modificó las expresiones agregando el famoso término de la corriente de desplazamiento, de forma tal que las ecuaciones del electromagnetismo conserven la carga eléctrica total:

Como vimos en clase, de izquierda a derecha y de arriba hacia abajo, estás ecuaciones se obtienen respectivamente de la fuerza de Coulomb, de los experimentos de Faraday (que Maxwell escribió en esta forma), de la no observación de cargas magnéticas, y de las observaciones de Ampère. El último término en esta ecuación fue agregado por Maxwell para conservar la carga. Y aquí aparece la genial Emmy Noether:

Uno de los teoremas más importantes en la física teórica moderna, el teorema de Noether, nos dice que cada ley de conservación está asociada a una simetría. ¿A qué simetría se asocia la conservación de la carga? Resulta que esta conservación está asociada a la simetría de gauge del electromagnetismo. Sabemos que, por ejemplo, podemos sumarle una constante C a cualquier potencial φ, y obtener el mismo campo eléctrico E:

Es decir, podemos elegir arbitrariamente el cero del potencial. Y también sabemos que el trabajo necesario para desplazar una carga q entre dos puntos 1 y 2 con diferentes valores del potencial es W = q(φ₂ – φ₁). Luego, si fuera posible crear cargas de la nada, el trabajo necesario para crear una carga en un punto cualquiera debería ser qφ. Pero esto nos permitiría determinar el valor absoluto del potencial electrostático φ (¡y determinar en forma absoluta el cero del potencial!) simplemente midiendo el trabajo necesario para crear la carga q. Así, la conservación de la carga y la libertad de gauge del electromagnetismo están relacionadas: si la carga total no se conserva, podemos determinar en forma única el cero de los potenciales.

La conservación de la carga implica que no podemos cambiar la cantidad total de carga en el universo. Pero esto no implica que el universo tenga una carga eléctrica total igual a cero. Podría haberse originado con un desbalance de carga (por ejemplo, más cargas positivas que negativas), y por la conservación de la carga, el desbalance total de carga hoy debería ser el mismo que al inicio del universo. Pero toda la evidencia observacional hasta el momento indica que el universo es eléctricamente neutro. Por ejemplo, un desbalance de carga generaría campos eléctricos que impondrían una dirección privilegiada en el espacio y una anisotropía en la radiación cósmica de fondo, o una anisotropía en los rayos cósmicos que llegan a la Tierra. Nada de eso se observa. Si hay un desbalance de carga en el universo, debe ser muy pequeño.

La película es “La novia de Frankestein” (1935), y los monstruos son protagonizados por el mítico Boris Karloff Y por Elsa Lanchester. En la novela original de Mary Shelley el monstruo también pide que le construyan una pareja, o en caso contrario amenaza con matar a toda la familia del profesor Frankestein (un caso interesante y bastante literal de “publish or perish“). Pero el profesor Frankestein se niega a dar vida a otro monstruo. Sin embargo, en esta secuela a una película de 1931, el profesor hace lugar al pedido. La vida se insufla, tanto el monstruo como en su novia, con electricidad. La imagen de la novia de Frankestein, con su pelo en forma cónica y la onda blanca en forma de rayo a los costados, se ha vuelto una imagen icónica en la cultura popular. Todas las películas recientes sobre la historia de Frankestein no están a la altura de estas primeras películas: esta imagen, como la imagen clásica de Karloff en el papel del monstruo, con la frente amplia y los electrodos a los costados del cuello, se han vuelto imágenes de culto.

Mary Shelley escribió Frankestein en 1818. A fines del siglo XVIII Galvani y Volta hicieron una serie de experimentos en los que mostraron que hacer circular electricidad por la pata de una rana muerta contraía sus músculos, y la pata se movía. Los experimentos tuvieron un impacto importante en la cultura popular de la época e inspiraron a Mary Shelley. El descubrimiento tuvo también aplicaciones médicas en la electroterapia moderna, en el marcapasos, y el desfibrilador.

Los experimentos de Galvani y Volta forman parte de la serie de experimentos que entre los siglos XVIII y XIX establecieron las leyes fundamentales del electromagnetismo tal como hoy las conocemos. Y la serie de experimentos más influyentes fue realizada por Couloumb, Ampère, y Faraday. Couloumb usó materiales cargados eléctricamente y una balanza de torsión para determinar que la fuerza electrostática de atracción o repulsión entre las cargas es proporcional al producto de las cargas e inversamente proporcional a la distancia que las separa. Coulomb publicó tres trabajos con estos resultados experimentales a partir de 1785. La imagen de su balanza de torsión se muestra a continuación. Le permitió medir con mucha precisión la fuerza de atracción o de repulsión entre cargas, y poniendo las cargas a diferentes distancias (una sobre el brazo de la balanza de torsión, y desplazando libremente a la otra), mostrar que la fuerza decrecía con el cuadrado de la distancia que separaba a ambas cargas (básicamente, midiendo el ángulo en que se movía el brazo de la balanza):

Ampère hizo experimentos con cables, corrientes, y brújulas, continuando experimentos que fueron realizados primero por Ørsted en 1820. Ampère rápidamente se dio cuenta que la aguja de una brújula se alinea a lo largo de círculos concéntricos cuando la brújula me mueve en el plano perpendicular a un cable recto por el que circula una corriente. Y realizó experimentos para medir la fuerza entre dos cables rectos por los que circulan diferentes corrientes. Pero determinar una expresión para la fuerza magnetostática es mucho más difícil que en el caso electrostático considerado por Couloumb. La fuerza cambia de acuerdo a cómo se alinean los cables y a la dirección en la que circulan las corrientes, y construir evidencia experimental confiable requiere muchos más experimentos, con muchas más configuraciones (y muchos más papers), que los tres papers publicados por Coulomb a fines del siglo XVIII. Para comprender esto basta comparar la expresión moderna de la fuerza de Coulomb con la de la fuerza magnetostática en la ley de Biot-Savart (1820), ambas en el sistema de unidades cgs-Gaussiano:

Mientras que la primera fuerza solo involucra dos magnitudes escalares (las cargas q₁ y q₂, respectivamente en posiciones r₁ y r₂), la segunda expresión involucra magnitudes vectoriales asociadas a las direcciones de las corrientes I₁ e I₂ a lo largo de dos cables, y las integrales sobre todo el recorrido de ambos cables.

Algo parecido ocurrió con los experimentos de Faraday. Y el caso de Faraday brinda además un ejemplo interesante de cómo se comunicaba la ciencia en el siglo XIX, y cómo se sigue comunicando hoy. Entre 1821 y 1832 Faraday hizo una gran cantidad de experimentos estudiando el fenómeno de inducción, creando el primer generador (un dínamo), e identificando con éxito la relación entre corriente y voltaje. En su serie de experimentos más importante, condensada en la ley de Faraday en las ecuaciones de Maxwell, usó dos cables aislados para mostrar que al variar en el tiempo la corriente que pasa por uno de los cables, otra corriente es inducida en el segundo cable. Uno de sus experimentos se veía aproximadamente así:

Las dos bobinas (A y B) están enrolladas alrededor de un mismo núcleo, pero aisladas entre si. La corriente en la bobina A se hace variar en el tiempo conectando y desconectando la batería que se encuentra a la derecha. Y el galvanómetro G, a la izquierda, se usa para detectar la corriente inducida en la bobina B al conectar y desconectar la bobina A. Este tipo de experimentos suele contarse como si fueran experimentos demostrativos. Pero para determinar expresiones empíricas para las fuerzas eléctrica, magnética, y electromotriz, fue necesario construir y publicar grandes cantidades de tablas. Solo en la revista Philosophical Transactions of the Royal Society, Faraday publicó más de 30 papers y reportes con diferentes configuraciones y mediciones de sus experimentos, la mayoría de ellos en una serie de trabajos numerados con el título “Experimental researches in electricity” (¡y los papers fueron refereados por pares!). Es decir, ya en 1832 Faraday comprendía la importancia de publicar sus resultados (aunque fueran preliminares) luego de ser evaluados por colegas, y de comunicar lo aprendido brindando explicaciones de los detalles, las limitaciones de sus experimentos, valores para cada una de sus mediciones, y estimaciones de los errores experimentales. Más allá de las discusiones contemporáneas sobre “publish or perish” y las prácticas actuales (criticables) de ciertas editoriales científicas, el deseo por comunicar lo que uno descubre es atemporal, y la mayoría de los grandes físicos en la historia generaron gran cantidad de trabajos para sostener el diálogo con sus colegas, discutir, y aprender de los resultados de otros.

Los que quieran leer más sobre la historia temprana del electromagnéticos, y especialmente sobre los papers publicados por Faraday describiendo sus experimentos, pueden leer este paper reciente en Philosophical Transactions of the Royal Society:

• The birth of the electric machines

Finalmente, recuerden que a partir del lunes cambiamos el horario de teóricas y prácticas, de acuerdo a lo votado en clase. Las teóricas serán de 14 a 16 hs, y las prácticas de 16 a 19 hs.

En la novela “El resplandor (The shining)” de Stephen King, Danny Torrance es un chico con habilidades psíquicas: puede leer mentes, tener premoniciones, y hablar con fantasmas (como comentario al margen, yo viví por más de cuatro años en la misma calle en la que, en la novela, vive la familia Torrance, y a pocas cuadras del lugar en donde vive la familia en la película). La novela fue adaptada para el cine por Stanley Kubrick en 1980. La película, en la que Kubrick tomó varias libertades respecto a la historia original en la novela, es un clásico del terror psicológico que les recomiendo para el fin de semana. Y también fue genialmente homenajeada en un especial de Halloween de Los Simpsons (“Sin televisión y sin cerveza Homero pierde la cabeza”).

Como en El resplandor y en buena parte del cine de terror, los sucesos contrarios a lo que parece natural suelen generar horror o fascinación en las personas (o ambas cosas). No por nada Einstein catalogó a un extraño efecto cuántico como “spooky action at a distance” (o escalofriante acción a distancia). Y a lo largo de los siglos, la acción a distancia asociada a las fuerzas electromagnéticas, y la capacidad de mover cosas sin tocarlas, ha generado ambas reacciones en las personas. La gravedad es otro ejemplo de acción a distancia, pero las escalas involucradas son tan grandes que nos resulta más natural (o menos manipulable). Con las fuerzas electromagnéticas podemos controlar cosas en escalas humanas. Podemos usar un imán para atraer a la distancia a un material paramagnético, o usar al mismo imán para sostener un papel pegado a la heladera, algo que a todas luces es muy extraño (y para nada fácil de explicar). Claro que todos estos efectos no son inmediatos, se propagan a la velocidad de la luz. Actúan a la distancia, pero con una velocidad de propagación finita.

Aunque hoy nos parezca natural comunicarnos con ondas de radio (¡pero no a todo el mundo le resulta natural, y muchas personas divulgan teorías conspirativas sobre la llegada del 5G!), poder ejercer fuerzas a distancia generó miedo y pánico en muchas generaciones. No es casual que el profesor Frankestein haya dado vida a su monstruo usando electricidad, un tema al que regresaremos en un próximo post. Ni es casual la fascinación de Tesla y de los primeros escritores de ciencia ficción con el rayo de la muerte. Los reportes pseudocientíficos de actividad paranormal, avistamientos de OVNIs y poderes psíquicos suelen venir acompañados por variopintas descripciones de campos electromagnéticos, autos que se apagan espontáneamente, y ruido blanco en las señales de radio y televisión. Poder controlar a gusto campos electromagnéticos es, en el imaginario popular, algo sobrenatural (cuando la realidad es que esto es algo que hacemos diariamente). Y desde el miedo primitivo de nuestros antepasados a los rayos en las tormentas eléctricas, hasta el reciente uso por David Lynch del tendido eléctrico como un portal a otras dimensiones en Twin Peaks, el electromagnetismo ha sido para muchos un fenómeno misterioso que no debemos subestimar.

La teoría física del electromagnetismo tal como hoy la conocemos comenzó a gestarse a partir de experimentos que se realizaron a fines del siglo XVIII y en el siglo XIX. Hacia fines de ese siglo Maxwell condensó todos los resultados en las famosas ecuaciones que llevan su nombre, que en vacío y en el sistema de unidades cgs-Gaussiano toman la forma

Estas ecuaciones rápidamente permitieron descubrir nuevos fenómenos físicos, que encontraron aplicaciones que seguimos usando hoy. Ya no nos sorprende poder comunicarnos usando ondas de radio (¡o no debería!). Ni el uso de radares, o de antenas de celulares y señales de WiFi. Pero en esta materia deben volver a sorprendernos. Debemos ver el resplandor de estos fenómenos como Danny Torrance ve a los fantasmas. O, en palabras de Ray Bradbury en Crónicas Marcianas (1950),

“Es bueno renovar nuestra capacidad de asombro -dijo el filósofo-. Los viajes interplanetarios nos han devuelto a la infancia“.

Para entender los fenómenos físicos, debemos volver a preguntarnos qué ocurre en el contorno de un conductor perfecto, por qué el campo eléctrico es más intenso en el entorno de regiones con forma de punta en materiales conductores, y cómo son los campos dentro de un dieléctrico. Son preguntas sencillas, y de física clásica. Pero si podemos comprender esos fenómenos, la teoría electromagnética nos dará herramientas muy poderosas para entender fenómenos mucho mas complicados y que juegan un rol central en la física contemporánea, como la dinámica de los campos magnéticos en estrellas y galaxias, la razón por la cual las estrellas no están donde creemos que las vemos en el cielo nocturno, la física de metamateriales, por qué usamos capacitores cilíndricos, cómo se produce un rayo, o por qué el cielo en nuestro planeta es celeste. Todos estos fenómenos los estudiaremos en la materia, a lo largo de las clases o en posts en esta página web.

No dejen de ver el último notebook de Python y las instrucciones sobre cómo usarlo. Pierdan el miedo y úsenlos. No es necesario saber programar, no es necesario que lean largos tutoriales de Python, ni que se vuelvan expertos. Solo que se atrevan a escribir “diff(cos(x),x)” en alguno de los notebooks que les pasé con SymPy, y aprieten SHIFT+ENTER. ¡Atrévanse a volar! Todo es muy sencillo:

El electromagnetismo clásico es una teoría muy formal y elegante, pero que también puede resultar tediosa en algunos de sus aspectos matemáticos. A lo largo de la materia haremos muchas cuentas, y es fácil perder el foco pensando que la principal motivación del curso es la formalización, olvidando el origen experimental de la teoría electromagnética. O preguntarnos para qué necesitamos hacer tantas cuentas, o conocer tantas formas diferentes de resolver un mismo problema. Así que este primer post de las clases teóricas va a intentar motivar posibles respuestas a estas inquietudes, expandiendo algo que comenté en la primera clase del curso.

El primer video lo pongo en la página de muchos de los cursos que dicto (los que ya lo vieron pueden volver a verlo, porque siempre se puede volver a ver a Feynman). El video muestra una clase brillante de Richard Feynman explicando su visión sobre cómo se construye una teoría. Alcanza con mirar el primer minuto:

En el video Feynman dice que la búsqueda de una nueva ley física comienza “adivinándola” (“first, we guess it“). Luego se derivan consecuencias y predicciones a partir de esa ley “adivinada”, y se verifican (o no) esas predicciones con experimentos. Y a continuación Feynman es categórico: “If it disagrees with experiments, it is wrong. And that simple statement is the key to science. It doesn’t make a difference how beautiful your guess is, it doesn’t make a difference how smart you are, or who made the guess or what his name is, if it disagrees with experiments… it is wrong”. En física no hay argumentos de autoridad o de elegancia o belleza que valgan. Esto puede resultar sorprendente en vista a ríos de tinta que se han escrito diciendo lo contrario, pero es el núcleo central de la física concebida como una ciencia natural. Si la teoría está en desacuerdo con los experimentos, está mal. El resto del video continúa con Feynman hablando de platos voladores, pseudociencias, y otros conceptos del método científico. Si tienen tiempo, les aconsejo mirarlo completo. Y los que tengan ganas, pueden mirar el ciclo de charlas (con subtítulos) sobre “El carácter de la ley física” que Feynman dió en Caltech en 1964, del que el video que menciono arriba es solo un breve extracto:

• Richard Feynman’s Messenger Lecture Series.

La teoría electromagnética es un hermoso ejemplo de las ideas de Feynman sobre cómo funcionan las ciencias naturales. Por encima de la elegancia de las ecuaciones de Maxwell, la teoría se construyó a lo largo de muchos años a partir de los experimentos de Coulomb, Faraday, Ampére y muchos otros. Cada una de las ecuaciones de Maxwell sintetiza en forma elegante los resultados de esos experimentos. Y como veremos a lo largo del curso, la evidencia experimental compatible con esta teoría se enfrentó y desplazó a teorías físicas con mucha autoridad, elegantes, y asociadas a grandes nombres, como la mecánica Newtoniana.

¿Y entonces, para qué aprender a hacer tantas cuentas? ¿Para qué vamos a tener que poder reproducir estas cuentas en el examen final? ¿Para qué repetir paso por paso cuentas que ya hicieron otros? Y aquí Feynman también viene al rescate:

Esta es la foto del pizarrón en la oficina de Richard Feynman el día de su muerte. La frase mas citada de este pizarrón es “What I cannot create I do not understand”, pero la que nos va a interesar como motivación para este curso es la que aparece abajo: “Know how to solve every problem that has been solved”, o Saber cómo resolver cada problema que ha sido resuelto. A la derecha pueden ver una lista de problemas que Feynman quería aprender (“To learn”). Esa lista incluye al ansatz de Bethe (un método para encontrar soluciones exactas de un modelo simplificado para materiales antiferromagnéticos), el efecto Kondo (el cambio en la resistividad eléctrica de un metal por el scattering de los electrones en impurezas magnéticas), el efecto Hall en dos dimensiones, la temperatura que mide un observador acelerado en un problema relativista, e hidrodinámica clásica no-lineal. Uno de estos problemas (“Kondo”) aparece tachado, probablemente porque Feynman consideró que ya había comprendido suficientemente bien el tema.

A veces los físicos aparentan que las grandes ideas nacen exclusivamente de su propia genialidad (y Feynman no era ajeno a esta práctica). Pero este pizarrón nos da una visión más humilde y realista de cómo se hace física teórica, y ciencia en general. Feynman, aún a sus 70 años y luego de ganar un premio Nobel, se sentaba con los papers recientes en temas muy diversos, algunos muy lejanos a su área de trabajo, y aprendía a hacer las cuentas paso por paso (“Know how to solve every problem that has been solved”). ¿Por qué? Porque usualmente, cuando vemos un problema nuevo, reconocemos semejanzas con otros problemas que estudiamos y lo intentamos resolver usando las herramientas que aprendimos a usar en otras partes de la física. Muchos de los métodos que aprenderemos en esta materia (como el método de separación de variables, las funciones de Green, o las expansiones multipolares) forman parte de las herramientas que se usan todo el tiempo en física teórica, y aprender a manejarlos cómodamente es lo mínimo que podemos hacer luego de ver los esfuerzos que hacía Feynman a sus 70 años. Y para conseguirlo no hay grandes secretos, hay que sentarse y hacer los problemas de las guías de trabajos prácticos, hacer preguntas, consultar las dudas, y pasar horas ejercitando.

No dejen de ver el posteo previo con instrucciones sobre cómo usar Google Colab. Cómo a lo largo de la materia habrá muchos posteos como ese y como este, y la práctica también tendrá noticias y avisos que hacer, para facilitar la navegación vamos a marcar los posteos con categorías (“Teóricas”, “Prácticas” y “Novedades”). En el menú a la derecha en la página de la materia van a encontrar la lista de las categorías, y apretando en una de ellas podrán ver solo los posteos que correspondan a esa categoría. Recuerden que pueden canalizar cualquier duda, pregunta o crítica en los foros del Campus Virtual. Allí encontrarán varios foros ya creados para consultas sobre las clases teóricas, sobre la guía de ejercicios, y para hacer sugerencias. No duden en añadir nuevos temas de conversación en cada uno de los foros siguiendo las reglas que figuran en el campus.