(Corregido 3 A.M.) En la Guía 7, uno de los primeros problemas es analizar el espacio de fases reducido de una peonza simétrica, con un punto fijo y gravedad…(seguir leyendo “¡Eres una peonza!”)
En la Guía 7, uno de los primeros problemas es analizar el espacio de fases reducido de una peonza simétrica, con un punto fijo y gravedad…(seguir leyendo “¡Eres una peonza!”)
Monthly Archives: octubre 2017
Mathematica o la fuerza del amor
Hoy es un buen día para comprar el programa Mathematica y empezar a hacer pequeñas simulaciones. Como lo prometí en campaña, [aquí] les dejo un notebook para resolver el problema de las oscilaciones de 4 masas enhebradas en un círculo. Las animaciones siguientes fueron hechas con ese notebook. Fácilmente se puede cambiar el número de partículas.
Para fijar las condiciones iniciales en la animación de abajo (que es una mezcla de los 4 modos, incluido el de rotación rígida) se procedió a ingresar un niño 2D a la habitación y se le pidió que moviera a su gusto los controles del programa, con el siguiente resultado:
Las frecuencias de los modos son inconmensurables, así que no aspiramos a hacer un gif que se cierre sobre sí mismo.
Repetimos la experiencia anterior con un niño 3D, y obtuvimos la animación de abajo.
Guía Michelin
 El diccionario de la Real Academia Española, entre lustre que te lustre, y entre un esplendor y el siguiente nos tira la siguiente definición por la cabeza:
El diccionario de la Real Academia Española, entre lustre que te lustre, y entre un esplendor y el siguiente nos tira la siguiente definición por la cabeza:
guía
3. f. Tratado en que se dan preceptos para encaminar o dirigir en cosas, ya espirituales o abstractas, ya puramente mecánicas.
¡Ni que a propósito!
Me gusta, sin embargo, lo de ‘dirigir en cosas’. Podemos intuir una próxima edición:
guía
3. f. Coso en que se dan cosos para encaminar o dirigir en cosas, ya espirituales o coso, ya puramente coso.
Lo que nos remite a la entrada de hoy: la Guía 7. ¡Este es tu año, Guía 7!
Me explico:
Pobre Guía 7. La suya es una historia de profesores apurados, en los últimos días de noviembre, que tienen que hacer entrar 20 temas en 2 clases, a un ritmo de 1 tema por clase, con el consiguiente no caber temas o faltar clases. Muchos de sus ejercicios nunca fueron hechos por nadie. Su redacción recuerda un estilo barroco, por momentos indescifrable, entretejido aquí y allá con interpolaciones de autores anónimos muy posteriores, y en no pocos casos, muy anteriores al cuerpo principal de la obra. Arcaísmos tales como “cuaternión”, “fluxión”, “lemniscata” y “docente” revelan el habla corriente de la baja edad media. Más de una palabra adolece de una grafía peculiar, anterior al uso de la imprenta y de la difusión de las artes.
En esta nueva edición hemos modernizado la ortografía y las figuras. Hemos eliminado los pasajes en verso e introducido el uso de la numeración decimal. Esto entre multitud de detalles que no vale la pena registrar. La posteridad hará lo propio.
Suplemento XOR!
Un equipo interdisciplinario resolvió el primer parcial. ¡Mira [aquí] sus extraños resultados!
Llega a nuestra redacción el último número de la Física Journal Americana de. Un [artículo] se destaca entre todos. Su autor es el Dr. Bizarro, quien entre pelea y pelea con la Liga de la Justicia se dedica a la termodinámica en Portugal. Un sincero reconocimiento de nuestra parte a los valientes que, en el mismo número de la revista, se atrevieron a replicar el artículo del Dr. Bizarro, con frases tan temerarias como la que copiamos –desde ya que sin adherir– aquí abajo: Intuimos que a esta altura el Dr. Bizarro ya habrá hecho papilla a estos inconscientes.
Intuimos que a esta altura el Dr. Bizarro ya habrá hecho papilla a estos inconscientes.
Atención Pablo V. Entre otras sorpresas que nos reserva el mentado número del Médico Jornalero Americano, hallamos una nueva instancia de la eterna disputa φ - π/2 vs φ, esta vez en el ámbito de la magnetostática:
No se dejen ser o estar. Recién vamos por la primera guía después del parcial. Fíjense como propósito resolver 2 o 3 problemas por día. Si se traban en alguno, consulten por mail.

Esta no es la actitud
¡Bienvenida a la Argentina, Guía 6!
 Pueden escucharla [aquí].
Pueden escucharla [aquí].
Incoming guía
Mientras esperamos el arribo a la Argentina de la Guía de pequeñas oscilaciones, [aquí] está el parcial del jueves pasado. Los alumnos prófugos (alias “Análisis dimensional”, alias “Calculadora Recursiva”, alias “Potencial 1/r a la quinta”, entre otros), podrían considerar resolverlo y, por qué no, entregarlo, sin compromiso.
Dónde, quién, cómo, cuándo
Primer parcial. Hoy a las 17 hs. Aula 10, la de siempre. Hasta agotar las localidades. Dos problemas sin rebuscamientos. Se puede usar regla de cálculo.
En el mismo instante, el hombre cuyas predilecciones iban hacia las perinolas comenzó a girar por la estancia con inmensa energía, abiertos los brazos en ángulo recto con el cuerpo, con lo cual se parecía realmente a una peonza, y derribando a todo aquel que se le ponía en el camino.
Edgar Allan Poe, El sistema del doctor Tarr y del profesor Fether.
Nota al pie de la pág. 133
Ya nos hemos encontrado varias veces con esta pequeña dificultad: el ángulo de Euler φ puede servir tanto para dar la orientación del cuerpo rígido como para definir la posición del centro de masa o de algún punto en particular, como ser el extremo de una varilla o el centro de la base de un cono. Es decir, a veces el ángulo φ, considerado como una coordenada generalizada, define más de una cosa. Uno está acostumbrado a pensar entonces que el punto en cuestión debe estar orientado según el versor eρ(φ), en polares, o el versor er(φ, θ), en esféricas. Ocurre que por lo general no es así. El centro de la base de un cono, con ángulos de Euler φ y θ, tomando el eje 3 según el eje del cono, está en la dirección definida por el ángulo azimutal φ-π/2. [Aquí] desarrollamos esta idea en un par de páginas, respaldándonos con citas de Landau. Ayer no hubo nadie que no consultara algo directamente relacionado con esto.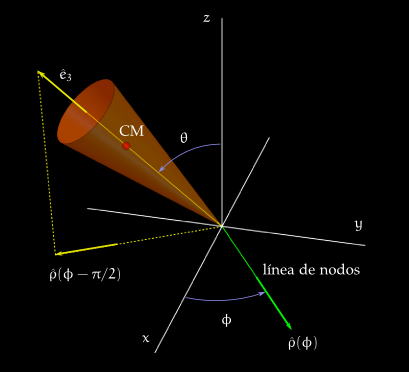
Hoy lunes
Empezamos a las 17 con la práctica previa al parcial. En principio, puras consultas, pero si se ponen de acuerdo entre ustedes, hacemos algún problema en el pizarrón y, después, karaoke. Doy fe de que respondemos consultas por mail, y hasta pasamos el corrector ortográfico y chequeamos la bandeja de salida para ver si no quedó como borrador, en cuyo caso lo enviamos de nuevo, pero pedimos disculpas por si llega repetido. Si están trabados en algo, quizá unas pocas palabras hagan la diferencia.
99 trucos sencillos de nuestras abuelas para resolver todos los problemas de cuerpo rígido
Él me miraba con ojos enormes, ¡no sabía qué cosa era el centro de gravedad…! (seguir leyendo los 99 trucos de nuestras abuelas sencillas para resolver todos los problemas de cuerpo rígido…)

