Ayudas para el parcial
Se acerca el parcial. Aclaramos que es a libro cerrado y sin hoja de fórmulas. Pero hoy es, además, una fecha especialísima. En el santoral del 18 de septiembre está José de Cupertino, patrono de los estudiantes.[Aquí] pueden leer la oración de pedido de ayuda para los exámenes, útil para todas las materias; no se aprovechen de su nobleza, dejen un poco del santo para los demás. Bioy Casares, en su segunda contribución a esta página, reseña así su vida y milagros:
José de Cupertino. Nació en 1602, en Cupertino, pueblito napolitano. Su familia era muy pobre. Porque no tardó en demostrar incapacidad para el estudio, sus padres lo sacaron de la escuela y lo colocaron de aprendiz de remendón; era tan desmañado que no logró aprender el oficio. A los 17 años entró como hermano lego en un convento franciscano; al poco tiempo lo despidieron, por inservible. Trató de ingresar en la orden de los Capuchinos, pero lo rechazaron. En 1621, por la recomendación de un tío suyo, lo admitieron en Santa María de Grosella, como oblato. Allá los padres superiores comprendieron pronto que, en su caso, la santidad se escondía bajo la rudeza y lo consideraron digno del sacerdocio.
El estudio fue para él un verdadero suplicio, porque sus facultades mentales eran escasas; sin embargo, pasó los exámenes milagrosamente y fue ordenado el 18 de marzo de 1628. Se retiró a orar. Durante los arrobamientos permanecía en suspenso en el aire, en suave levitación; por esto y por los milagros que le atribuyeron, intervino el Santo Oficio. Fue largamente examinado y se llegó a la conclusión de que no había “nada censurable en fray José”. Murió, como lo había predicho, el 18 de septiembre de 1663. Clemente XIII lo canonizó. Es patrono de los estudiantes y también, por ser llamado el Santo Volador, de los aviadores.
(En Descanso de Caminantes, de Adolfo Bioy Casares.)
Clases prácticas de ayer y de hoy
- La clase del jueves pasado en prolija versión autógrafa, puede bajarse [aquí].
- La clase de hoy, en impersonal tipo de letra Palatino generada por ordenador, está [acá] [revisada 17/9].
- Los ejercicios propuestos en la clase de hoy: encontrar la ecuación de la órbita para el potencial de Kepler repulsivo. Encontrar la sección eficaz diferencial para el potencial repulsivo k/r2, con k > 0.
- Propuesta mucho más difícil: encontrar la sección eficaz para el potencial atractivo V = -k/r2, con k > 0. Ahí la función b(θ) es multivaluada.
- Tip: en el problema del oscilador isótropo, usen el cambio de variables w = 1/r2 en la ecuación de la órbita.
- Abajo, un problema que permanece abierto:
Órbitas indebidas
El viaje había resultado agotador para el hombre (Oswalt Henry) y para la máquina. Por una falta del mecanismo o por un error del astronauta, entraron en una órbita indebida, de la que ya no podrían salir. Entonces el astronauta oyó que lo llamaban para el desayuno, se encontró en su casa, comprendió que la situación en la que se había visto era solamente un sueño angustioso. Reflexionó: Había soñado con su próximo viaje, para el que estaba preparándose. Tenía que librarse cuanto antes de esas imágenes que aún volvían a su mente y de la angustia en que lo habían sumido, porque si no le traerían mala suerte. Esa mañana, tal vez por la terrorífica experiencia del sueño, valoró como es debido el calor del hogar que le ofrecía su casa. Realmente le pareció que su casa era el hogar por antonomasia, el hogar original, o quizá la suma de cuanto tuvieron de hogareño las casas en que vivió a lo largo de su vida. Su vieja niñera le preguntó si algo le preocupaba y lo estrechó contra el regazo. En ese momento de supremo bienestar, Henry, el astronauta, entrevió una duda especulativa que muy pronto se convirtió en un desconcertante recuerdo; su vieja niñera, es claro, había muerto. “Si esto es así, pensó, “estoy soñando”. Despertó asustado. Se vió en la capsula y comprendió que volaba en una órbita de la que ya no podría salir.
Oswalt Henry, viajero, Adolfo Bioy Casares, en “Una magia modesta”.
Mucho muy importantes cosas
- La clase práctica del lunes 9/9, con algún que otro tema inédito, puede escucharse [aquí]. [revisada el 13/9]
- Recomendación: los dos problemas que hicimos en la clase del lunes para el potencial gravitatorio tienen su análogo para el potencial armónico en los problemas 4 y 5 de la Guía 4. Sería una buena idea que trataran de resolverlos siguiendo la misma línea de razonamiento.
- [Aquí] un paper que muestra que no todo es hacer integrales.
- Una guía atrás en el tiempo: más sobre potenciales giratorios, en la página de 2017, [aquí]. Ahí pueden encontrar papers con la demostración del teorema de Noether en el contexto de la Mecánica Clásica (su contexto original era otro).
- La animación que encabeza: es una órbita cerrada que resulta de modificar el problema de Kepler con un término en el potencial de la forma c/r2 . El punto de vista está por encima del plano de la órbita. Aunque se diga que es una elipse cuyo eje va rotando, claramente se ve que para precesiones tan grandes esa interpretación no se ajusta demasiado a la realidad.
Guía 4: Fuerzas centrales y dispersión
- La nueva guía acerca de fuerzas centrales y dispersión puede bajarse [aquí].
- Nueva en el sentido de que sus problemas han sido permutados, palabras han sido permutadas, items han sido permutados.
- También tiene nuevos problemas.
- Empezamos el lunes.
- Para los que extrañan, es como un breve retorno a Física 1.
- Falta poco para el parcial.
- Ya tendrían que estar terminando la Guía 2, alternándola con problemas de la Guía 3.
- Si se traban en un problema o no tienen la menor idea de por dónde empezar, también nos pueden consultar por mail. Sin compromiso de ninguna parte.
- Abajo, imagen de Kepler comiendo sushi en Praga, con un ojo en Marte y el otro en Júpiter.
¿Tienen los tigres potenciales rayados?
Todo muy lindo la clase de ayer, pero nadie interpuso ningún reparo cuando, al resolver los ejemplos del problema 10 de la Guía 3 (leyes de conservación para el movimiento de una partícula en el potencial gravitatorio de ciertas distribuciones de masa), adjudicamos a los potenciales las mismas simetrías que sus fuentes. Que una esfera produce un potencial que se parece a una esfera es algo evidente. Pero ¿es tan evidente en el caso de la distribución de masa con forma de hélice que el potencial tiene la forma de la hélice? ¿Hasta dónde podemos llegar por esa ruta? ¿Tiene cuatro patas y mueve la cola el potencial gravitatorio de un perro?
Todas estas preguntas, que poco o nada importan para resolver los problemas de las Guías, han sido glosadas en las notas que pueden bajar [aquí]. Abajo, el potencial de una hélice.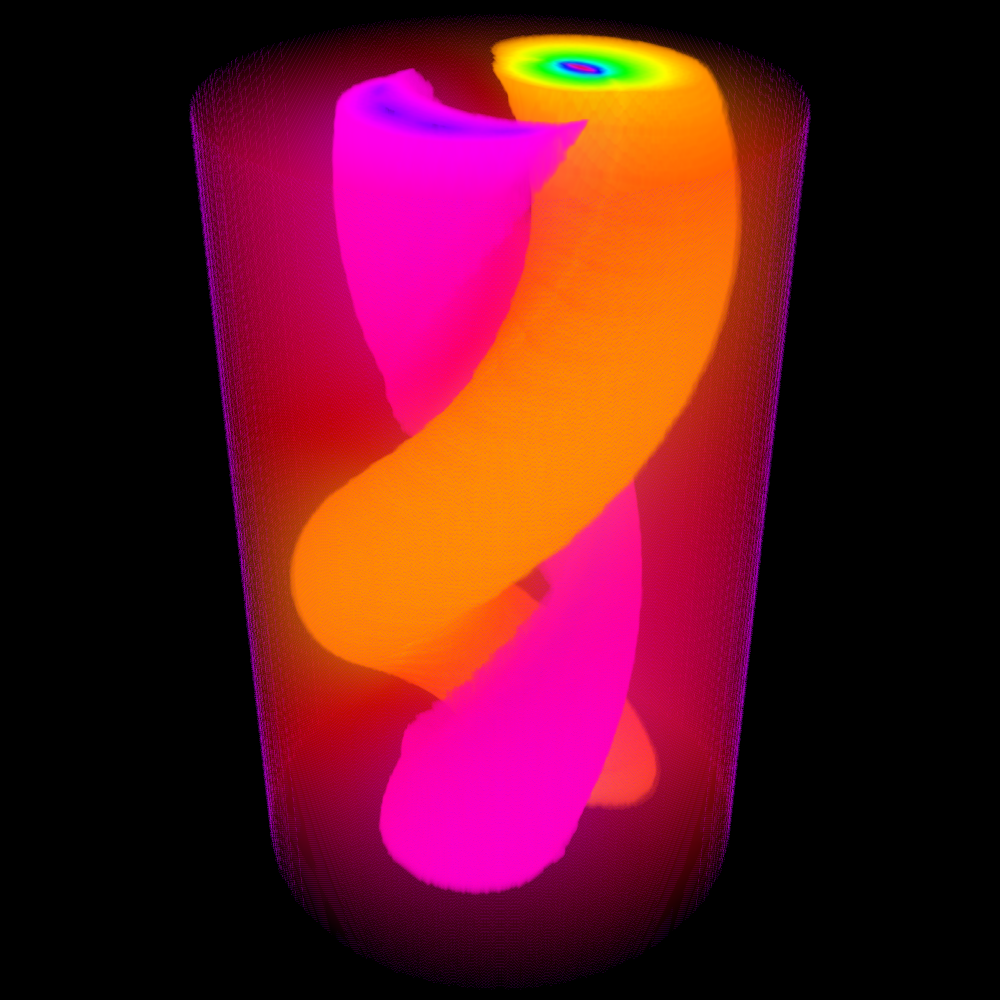
La clase práctica de hoy mismo
Si sos alumno con plan Goldstein® y tenés tu cuota al día, ya podés bajar la clase de hoy en pdf, [aquí]. Si no, podés intentar bajar una versión con errores colocados intencionalmente en los pasos clave, [aquí].
Abajo, cuadro de Hernán Cortés quemando la Guía 1 y sellando toda vía de escape a Física 1.
Clase práctica del jueves 29/8
[Revisada 1/9] Breve en el papel, extensa en su exposición. La pueden bajar [aquí] (prestar atención a las ecs. 12-14, que en clase me parece que las escribí mal). El video, de la Universidad Nacional de Córdoba, ilustra la transición entre la solución catenoide y la solución de Goldschmidt.
En otro orden de cosas:
- Al final de la clase de hoy quedó abandonada una tarjeta Sube.
- La inscripción a las materias del segundo cuatrimestre abrirá nuevamente desde el 2 hasta el 8 de septiembre. Yo no perdería la oportunidad de desinscribirme.
Historias mínimas
El jueves 29/8, en la práctica empezaremos a ver cálculo variacional, con cuestiones tan originales como la constante de la lemniscata, el límite de Laplace, burbujas, cadenas y un corto etcétera. Todo sobre la nueva Guía 3, [aquí].
Libro recomendado, por lo ameno e interesante: Stories about Maxima and Minima, de V. Tikhomirov. Lo tenemos en la librería, con una gran tapa. Link en la imagen para más cosas sobre rusos y máximos. 


 Follow
Follow





