• Fue un repaso de cuerpo rígido a través del problema del girocompás, para bajar [aquí]. En la wikipedia lo resuelven [reprime la risa] con matrices de rotación; lo digo para que comparen. Pueden hacerse de un girocompás en M*rcado Libre [aquí]. Se aceptan donaciones.
• La solución completa del problema del Planeta X puede bajarse [aquí].
• Para resolver los dos últimos problemas de la Guía 8 necesitarán escribir el hamiltoniano relativista en coordenadas polares. [Aquí] figura la respuesta, pero también queda planteado como ejercicio extra.

• Del ejercicio de ayer, [aquí] pueden bajar lo que resolvimos en clase. Hagan el resto. En unos días lo subo completo.
• El lunes es feriado. Si tienen consultas, háganlas por mail.
• El jueves que viene hay clase teórica, con el único cambio de que la práctica empieza a las 10:30.

Antes que nada, [aquí] pueden bajar la clase práctica del lunes 11. Aprovechen. Llevan relatividad y llevan también Hamilton-Jacobi.

Mañana vamos a ver en la clase práctica un problema de relatividad  sin transformaciones de Lorentz ni cuadrivectores. [Aquí] está para bajar. Sería bueno que lo leyeran y que tratasen de entender qué es lo que se pregunta. También podrían resolverlo. Tiene cero cuentas difíciles, pero las que tiene pueden producir calambre cerebral. Lo van a entender mejor si hacen antes el problema 4 de la Guía 8. ¿Qué les cuesta? Es un objetivo a corto plazo, dentro de las posibilidades de comprensión de un alumno pre-Mecánica Clásica, apenas si requiere transformaciones de Lorentz y los deja preparados para entender mejor el problema de mañana. Es pura ganancia.

Muerte por Exogorth y otros peligros que acechan a la vuelta de la esquina. Lo que tu Gobierno no quiere que sepas, encontralo en la nueva [Guía 8] de relatividad especial.Vea el mundo con ojos de borracho veloz. [juego interactivo]La clase del jueves pasado, un poco abreviada, [aquí]. La digresión que hicimos sobre el cuadrivector número de onda está desarrollada [aquí] (era Física Teórica 1, así que no se asusten si aparece un campo eléctrico).

• En primer lugar, un apunte con el problema resuelto durante la clase del lunes pasado. Es el problema 20 de la guía 7. Para bajar [aquí]. Apenas 8 páginas entre enunciado, figuras, solución y espacios en blanco. Nuestra consigna es “salvemos a los bosques”.
• Los problemas de la Guía 7 acerca de las variables de ángulo-acción pertenecen todos a la misma especie. Goldstein los despacha en media docena de ecuaciones. La práctica requiere, sin embargo, un proceso de familiarización. Pero, una vez cumplido, todos los problemas se resuelven más o menos en los mismos 3 o 4 pasos. Esos pasos están explicados con todo detalle en [este apunte]. Un mamotreto de 24 páginas a todo color cuya impresión arrastrará consigo más de una hectárea de bosque tropical.
• Siempre la parte más interesante de estos problemas es ver con qué diseño nos sorprenden las curvas coordenadas de las variables de ángulo-acción. Abajo, por ejemplo, está el caso del movimiento radial de Kepler.
• Es un simple ejercicio demostrar que la variable ángulo asociada al movimiento radial acotado del problema de Kepler (exceptuando la órbita circular) coincide a menos de un factor con el área barrida por el radio vector. ¿Se acuerdan de la ley áreas iguales en tiempos iguales? En este sentido, el avance de la variable ángulo de la Tierra durante un día es siempre el mismo, en tanto que el avance del ángulo que define su posición sobre la órbita (el ángulo de las coordenadas polares) depende del día.
• Y es una notable falta que en la mayoría de los libros se omita decir que las variables de ángulo-acción, al menos en los problemas unidimensionales, no son más difíciles de entender que las coordenadas polares en el plano. Las transformaciones canónicas permiten cambios de variables tan extraños que es comprensible no entender qué significan, por ejemplo, las nuevas coordenadas Q = Log[sin p/q] y P = q ctg p. Pero esto no es excusa en el caso de las variables de ángulo-acción.
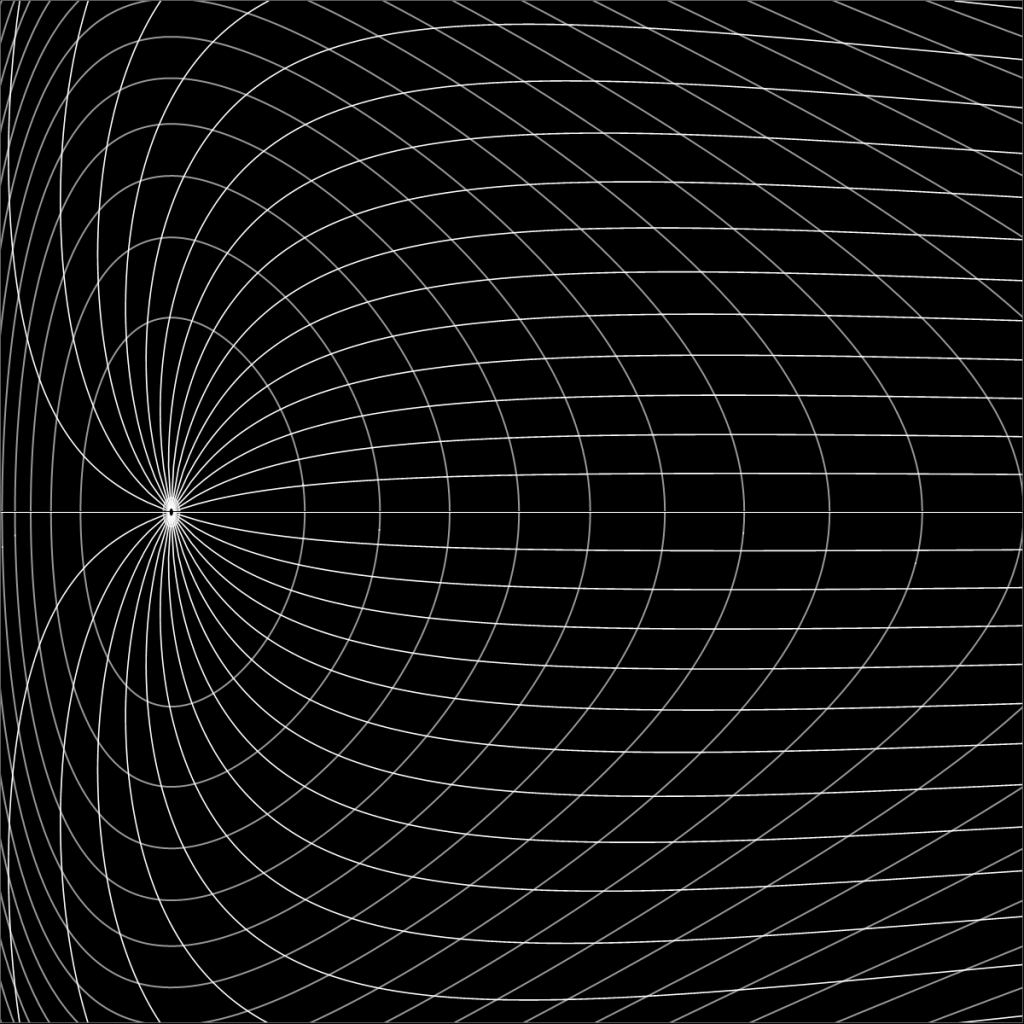
• No todos los retratos de fase son simétricos respecto al eje q. Es muy fácil hacer transformaciones canónicas que deformen el retrato de fase hasta llevarlo a formas fantásticas. Un caso que brilla por su falta de espectacularidad, pero que sirve para presentar esta cuestión, es el de una rotación en el plano qp. Con esta transformación el retrato de fase del oscilador, por ejemplo, toma típicamente el siguiente aspecto. En este caso es H = p² + p q + q². ¿Cómo se escriben en este caso las integrales que definen a la función característica de Hamilton y a la variable ángulo? ¿Cuáles son los puntos de retorno? ¿Cómo hay que dividir la órbita para que en cada tramo queden funciones univaluadas de q? Eh.
• Las variables de ángulo-acción de navidades pasadas (la notación cambió levemente): [2017 2c], [2018 1c], [2018 2c].
• Un libro en donde se toman la molestia de dar algunos ejemplos del cálculo de las variables de ángulo-acción: el de Percival y Richards (a la teoría la encaran por otro lado).

Ahora toca responder a ciertas graves denuncias que se han hecho circular en el aula.

• El problema 9 de la Guía 7 no tiene ningún error. No se dice nada de la dependencia explícita de f con el tiempo simplemente porque no tiene importancia decirlo.
• En el problema 3 es cierto que falta aclarar que es la componente z del momento angular la que se conserva.
• El problema 16 se resuelve por separación de variables. Busquen W(q₁, q₂) = W₁(q₁) + W₂(q₂). Contrariamente a lo que sugiere el enunciado, no intenten calcular las integrales. Resuelvan todo lo que se les dice, pero dejen sus resultados en términos de expresiones integrales. La parte interesante es la pregunta final.
• En el problema 17, en la expresión del hamiltoniano, E tiene que aparecer con signo menos. (Se editó el cambio en la guía que está subida).
• En el problema 18, si les queda una integral al cuadrado, pues les queda una integral al cuadrado. No hay ningún signo mal.
• Supongo que no avanzaron más allá, porque hasta ese problema me hicieron consultas.
• Y todavía falta subir la guía de relatividad.

Ya tengo medido que por clase entran alrededor de 60 ecuaciones. Las notas taquigráficas de la clase ayer suman 63. Se pueden bajar [aquí]. Después de terminada la clase me di cuenta de que sus protestas respecto a la deducción del sentido de giro de la partícula del problema 22 eran fundadas. En el apunte eso está corregido.

Ayer no llegamos a ver más que un ejemplo del método de Hamilton-Jacobi, pero en el camino surgieron varios detalles técnicos. Podrían estar haciendo los problemas 15-19 y el 22. Las notas de la práctica de ayer pueden bajarse [aquí]. Es de lo mejor que se ha escrito sobre el tema en la cuadra en la que vivo. Si quieren leer el ejemplo de ayer de otra fuente, en el libro de Hand y Finch tienen resuelto el problema de la partícula en el campo gravitatorio uniforme en tres dimensiones. De este libro la siguiente cita me parece pertinente

It is good to realize that the Hamilton-Jacobi equation is more of a theoretical framework than a specific algorithm for solving problems.

La teoría de Hamilton-Jacobi nació de la óptica, y muchas de las interpretaciones que se pueden hacer de la función S están relacionadas con la propagación de ondas. Esto lo digo más que nada para justificar la foto que sigue (click en la imagen para ampliar).

• [Aquí] pueden bajar las notas de la clase práctica de ayer.
• [Aquí], unos interesante problemas de cuerpo rígido, de un tipo diferente a los de la guía. El problema 5 es muy raro.
• En el video a continuación tienen una demostración práctica del problema 16 de la Guía 6, que trata sobre el Teorema del Eje Intermedio, con entretelones de la guerra fría.

La Guía 7 [corregido error p. 17; signo de E], acerca de ecuaciones de Hamilton, el método de Hamilton-Jacobi y las variables de ángulo-acción, puede bajarse [aquí]. No se atrasen, porque es una guía extensa.

Un error que varios advirtieron en el problema 7 de la Guía 6 (el problema del disco que es lanzado hacia arriba, también llamado disco de Feynman). El enunciado decía incorrectamente que la frecuencia de la función θ(t) era el doble de ω₀. El item (d) debió decir

Ya subimos la versión actualizada. Fíjense que lo que dice el enunciado es lo que sucede en esta animación, aunque en realidad el dibujo que hace e₃ en el problema de la guía es un cono cuyo eje está inclinado respecto al eje z. Dibujen este cono para entender mejor lo que está haciendo  e₃ y ver cómo es posible que e₃ de dos vueltas por cada vuelta que dan e₁ y e₂, lo cual es aparentemente contradictorio. Uno tiende a pensar que los tres versores deberían girar con la misma frecuencia, llevados por el ángulo  φ.

No sólo de la invención de la Birome y del dulce de leche se vanaglorian los húngaros. El Gömböc es otro de sus inventos nacionales: un sólido tridimensional, homogéneo y convexo que cuando reposa sobre una superficie plana tiene un solo punto de equilibrio estable y un solo punto de equilibrio inestable. En dos dimensiones eso es imposible. En tres dimensiones su existencia fue conjeturada por V. Arnold en 1995 y demostrada por los húngaros Gábor Domokos y Péter Várkonyi en 2006. Lean el artículo de la [wikipedia], busquen al Gömböc en youtube o visiten este [link], donde se nos explica que Gömböc se pronuncia goemboets, pero nada se nos dice de cómo se pronuncia goemboets. Allí también pueden encargar uno por muy pocos euros. En M*rcado Libre no lo tienen. Yo encontré interesante este [video]. (No se por qué esta [entrevista] a uno de sus descubridores aparece relegada en la lista de resultados; detecto gran similitud entre el magiar y el japonés).

Otro animal esférico es el [oloide]. No es fácil imaginárselo, aún viendo la foto de un oloide en cautiverio. Aquí tienen un video de un oloide en su hábitat:

Por último, al final del apunte con la [clase práctica de ayer], encontrarán la descripción de otro animal esférico, tan grande que no se puede apreciar a simple vista.